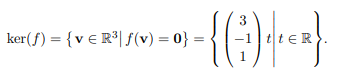Lineare Abbildungen

Eine Lineare Abbildung ist definiert durch:

Längen treue (längentreue) Lineare Abbildungen

Bekommen wir durch: $A^T\cdot A=E_n$ was auch einer Orthogonal Matrix beschreibt.

Abbildungsmatrix bestimmen

Einstetzen der Standard Vektoren in die Abbildung

$f:{\mathbb{R}}^{\mathbb{3}}\mapsto {\mathbb{R}}^{\mathbb{3}}|f(x,y,z)=\left[\begin{array}{c}x+2y-z\\ y+z\\ x+y-2z\end{array}\right]$

$f\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)$ = $\left[\begin{array}{c}1+0+0\\ 0+0\\ 1+0+0\end{array}\right]$ = $\left(\begin{array}{c}1\\ 0\\ 1\end{array}\right)$

$f\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)$ = $\left[\begin{array}{c}0+2+0\\ 2+0\\ 0+2+0\end{array}\right]$ = $\left(\begin{array}{c}2\\ 2\\ 2\end{array}\right)$

$f\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$ = $\left[\begin{array}{c}0+0-1\\ 0+1\\ 0+0-2\end{array}\right]$ = $\left(\begin{array}{c}-1\\ 1\\ -2\end{array}\right)$

Resultat:
$A=\left[\begin{array}{ccc}1& 2& -1\\ 0& 2& 1\\ 1& 2& -2\end{array}\right]$

Kern einer Linearen Abbildung

Injectivität: Dass 2 verschiedene V auf W abgebildet werden.
Surjectiv: todo

Kern bestimmen

1. Abbildungsmatrix bestimmen
2. Abbildungsmatrix 0 setzten
3. Mittels Gaus lösen

Bild einer Linearen Abbildung

heisst auch Spaltenraum

Beispiel

gegeben sei $f:{\mathbb{R}}^2\mapsto {\mathbb{R}}^3,mit\left[\begin{array}{c}x\\ y\end{array}\right]\mapsto \left[\begin{array}{c}x+y\\ x-y\\ x+y\end{array}\right]$

$IM(f)=L(f(e1),f(e2)=L(f(\left[\begin{array}{c}1\\ 0\end{array}\right]),f(\left[\begin{array}{c}0\\ 1\end{array}\right]))=L(\left[\begin{array}{c}1+0\\ 1-0\\ 1+0\end{array}\right],\left[\begin{array}{c}0+1\\ 0-1\\ 0+1\end{array}\right])$

Beispiel 2

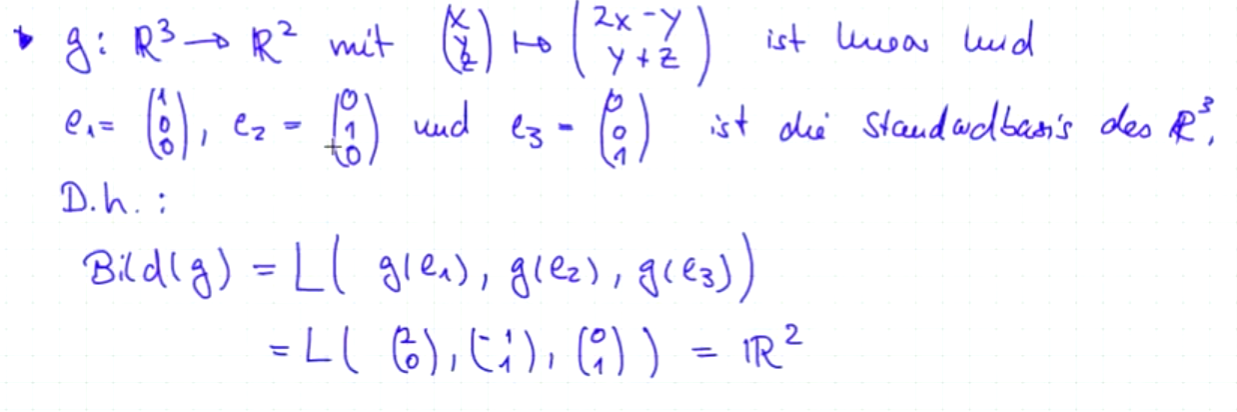
Beispiel 3 ALA

gegeben folgende Abbilungsmatrix = $A=\left[\begin{array}{ccc}1& 2& -1\\ 0& 1& 1\\ 1& 1& -2\end{array}\right]$

Spalten als Spaltenvektoren darstellen:

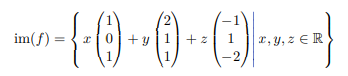
Nun haben wir das Bild, jedoch mit linear Abhänigen Vektoren. Hier sieht man nicht, dass das Erzeugersystem eigentlich ein ${\mathbb{R}}^{\mathbb{1}}$ ist anstatt ein ${\mathbb{R}}^{\mathbb{3}}$. Deshalb lösen wir die Vektoren als Gleichungssystem:

TR: sys-solve: $\left[\begin{array}{cccc}1& 2& -1& 0\\ 0& 1& 1& 0\\ 1& 1& -2& 0\end{array}\right]$

Lösung:
x = 0 + 3z
y = 0 - z
z = z

Ergibt ein Vektor: