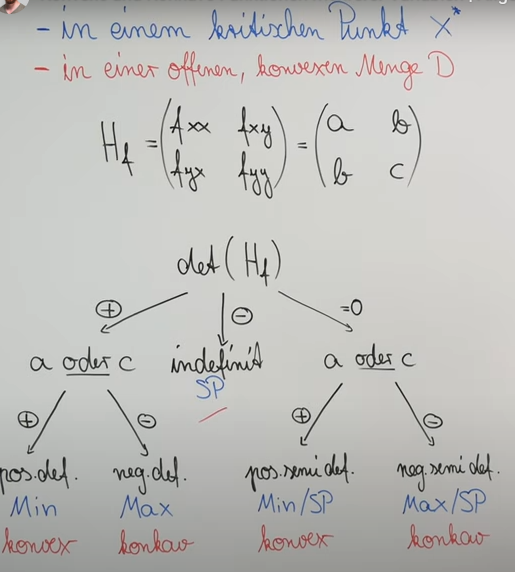
Die Hesse-Matrix ist ein Werkzeug in der Analysis, das verwendet wird, um das Verhalten einer Funktion an kritischen Punkten zu analysieren. Sie besteht aus den zweiten partiellen Ableitungen der Funktion und hilft dabei, das Vorhandensein von Maxima, Minima oder Sattelpunkten zu bestimmen.

Hesse-Matrix Definition:

• Größen:
  • $H_f$: Hesse-Matrix
  • $f_{xx},f_{yy}$: Zweite partielle Ableitungen von $f$ nach $x$ bzw. $y$
  • $f_{xy},f_{yx}$: Gemischte zweite partielle Ableitungen
  • $a,b,c$: Elemente der Hesse-Matrix

Determinantenanalyse:
Der Determinant der Hesse-Matrix hilft dabei, die Natur der kritischen Punkte zu bestimmen.

Determinantenregel:

Analyse der Determinante:

• Wenn $det(H_f)>0$:

  • Wenn $a>0$: Lokales Minimum (positiv definit, konvex)
  • Wenn $a<0$: Lokales Maximum (negativ definit, konkav)

• Wenn $det(H_f)<0$: Sattelpunkt (indefinit)

• Wenn $det(H_f)=0$:

  • Weiteres Testen erforderlich (positiv semidefinit oder negativ semidefinit)

• Größen:

  • $det(H_f)$: Determinante der Hesse-Matrix
  • $a,c$: Elemente der Hesse-Matrix, die die zweiten partiellen Ableitungen darstellen
  • Sattelpunkt (SP)

Beispiel:
Betrachten wir eine Funktion $f(x,y)$ mit den folgenden zweiten partiellen Ableitungen:

Die Hesse-Matrix ist:

Die Determinante der Hesse-Matrix ist:

Da $det(H_f)>0$ und $f_{xx}=2>0$, hat die Funktion ein lokales Minimum an diesem kritischen Punkt.