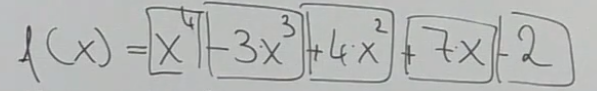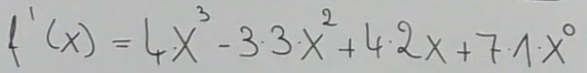Theorie
Ableitungsregeln
Ableitungsregeln
In der Differentialrechnung sind Ableitungsregeln von zentraler Bedeutung, um die Ableitung einer Funktion zu bestimmen. Hier sind einige grundlegende Ableitungsregeln und Beispiele:
Grundlegende Ableitungen:
- Größen:
: Funktion : Ableitung der Funktion : Konstante : Konstanten : Exponent : Natürlicher Logarithmus : Sinusfunktion : Kosinusfunktion
Weitere Beispiele:
Anwendung der Ableitungsregeln:
- Konstante Regel: Die Ableitung einer Konstante ist Null.
- Potenzregel: Die Ableitung von
ist . - Exponentialregel: Die Ableitung von
ist . - Logarithmusregel: Die Ableitung von
ist . - Trigonometrische Regeln: Die Ableitung von
ist und die Ableitung von ist . - Kettenregel: Wenn
und , dann ist die Ableitung von bezüglich gegeben durch . - Produktregel: Wenn
, dann ist die Ableitung . - Quotientenregel: Wenn
, dann ist die Ableitung .
Diese Regeln sind essentiell für die Berechnung von Ableitungen komplexer Funktionen und werden in vielen Bereichen der Mathematik und Naturwissenschaften angewendet.
Ableitungsregeln
Summenregel
Formel
Produkteregel
Formel
Quotientenregel
Formel
Kettenregel
Formel
Tricks:
-
Wurzeln umschreiben:
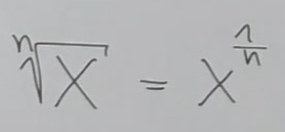
-
Brüche umschreiben:
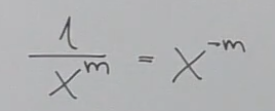
-
Wenn X im Nenner Steht
- Vorzeichen mal minus
- Exponent des Nenners 1 erhöhen
- Alter Exponent mal alter Zähler
Achtung Kettenregel beachten!!
Beispiele:
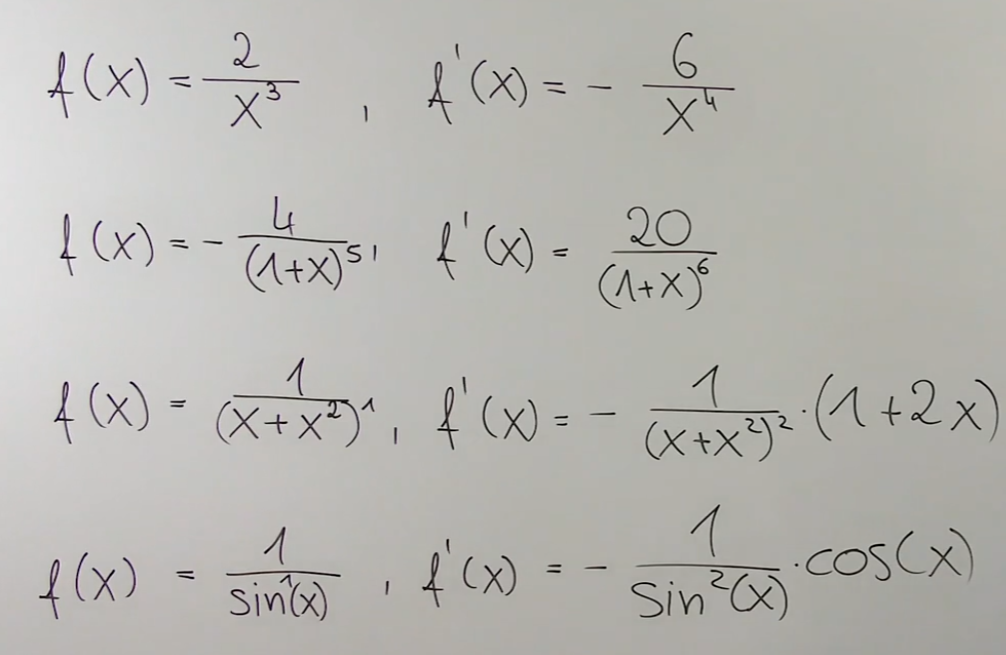
Differenzieren
Grundlagen
Polynome
Polynome werden so abgeleitet, dass jede einzelne Summe betrachtet wird und mittels Grundfunktionen abgeleitet wird.