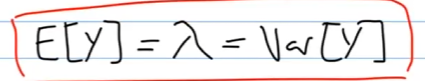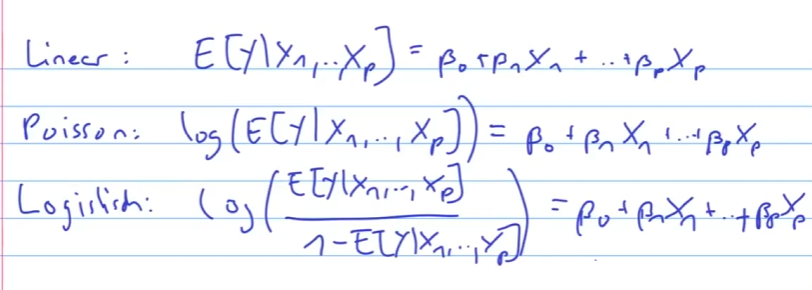Header
All videos:
(254) StatsLearning Lecture 1 - part1 - YouTube
Book:
!ISLP_websit__ISLP_website__e 1.pdf
![[ISLP_website (1).pdf]]
Statistical Learning
Overview of Statistical Learning
Statistical Learning umfasst Werkzeuge zur Datenanalyse. Es gibt zwei Haupttypen: supervised und unsupervised learning.
Supervised Learning
Was ist der Unterschied zwischen Regression und Classification?
?
Supervised Learning baut Modelle zur Vorhersage von Outputs (Y) aus Inputs (X):
Regression: Vorhersage eines quantitativen Outputs.
Classification: Vorhersage eines qualitativen Outputs.
Unsupervised Learning
Unsupervised Learning bestimmt Beziehungen aus Inputs (X), ohne supervisierte Outputs:
Clustering: Gruppierung basierend auf Ähnlichkeiten.
Association: Identifizierung von Regeln in Daten.
Lineare Regression
Was sind die Fehler Komponenten der STL
?
Das Hauptproblem ist, dass wir (Y) und (X) kennen, jedoch nicht die wahre Funktion (f):
(\epsilon) ist dabei das Rauschen bzw. der Messfehler.
Wir wollen eigentlich die Approximation herausfinden:
Warum schreibt man hier
- Welcher ist der reduzierbare Fehler? ::
) - Welcher Fehler ist der irreduzible Fehler? ::
)
Was ist die Bias Varianz Zerlegung
?
Die Bias-Varianz-Zerlegung hilft dabei, den erwarteten quadratischen Fehler einer Vorhersage zu verstehen. Sie teilt den Fehler in reduzierbare und irreduzierbare Komponenten auf. Der reduzierbare Fehler kann durch Verbesserung des Modells verringert werden, während der irreduzierbare Fehler durch Zufallsrauschen verursacht wird und nicht eliminiert werden kann.
ist der Erwartungswert ist die tatsächliche Zielvariable ist die vorhergesagte Zielvariable ist die wahre Funktion ist die vorhergesagte Funktion ist der irreduzible Fehler (Rauschen) ist die Varianz des irreduziblen Fehlers
Hier ist die Notiz zur Bias-Varianz-Zerlegung der mittleren quadratischen Fehlers:
Die Bias-Varianz-Zerlegung ist ein Konzept in der Statistik, das die erwartete quadratische Abweichung eines Schätzers (\hat{f}(x_0)) von einem tatsächlichen Wert (y_0) in drei Komponenten zerlegt:
- (
: Erwartete quadratische Abweichung : Varianz des Schätzers : Quadrat des Bias des Schätzers : Varianz des irreduziblen Fehlers
Es gibt 2 Ansätze für die Regression welche?
?
- Parametrische Methode (eg. Lineare Regression) -> Hat eine starke induktive Bias, ist aber sehr effizient mit nur ein paar Parameter
- nicht Parametrische Modelle (e.g KNN -> Gesetzt der Kontinuität, ) -> Flexibler, Können sich viel besser an Daten anpassen, kann aber schnell overfitten
Wie sehen die Tradoffs von Modellen?
?

Was ist der Bias :: zu viel BIAS ist undefitting
Was ist der Variance :: zu viel Variance is overfitting
Was ist der Bias Variance Trade off
?
Die Bias-Varianz-Zerlegung beschreibt, wie die Erwartung des quadratischen Fehlers einer Vorhersage durch die Varianz der Vorhersage, den Bias der Vorhersage und die Varianz des irreduziblen Fehlers beeinflusst wird. Diese Zerlegung hilft, die Fehlerquellen eines Modells zu analysieren und zu verstehen.
ist der tatsächliche Wert ist der vorhergesagte Wert ist die Varianz der Modellvorhersage ist der Bias der Modellvorhersage ist die Varianz des irreduziblen Fehlers
Was ist der Bayes Classifier
?
Der Bayes-Klassifikator im maschinellen Lernen nutzt die bedingte Wahrscheinlichkeit, um die Wahrscheinlichkeit eines bestimmten Klassenergebnisses
ist die Zielvariable oder Klasse ist ein spezifischer Wert oder eine Klasse, die annehmen kann ist die Merkmalsvariable ist ein spezifischer Wert oder Beobachtung, die annimmt
KNN
?
Der k-Nearest Neighbors (k-NN) Klassifikator ist eine einfache, nicht-parametrische Methode, die verwendet wird, um die Wahrscheinlichkeit zu berechnen, dass ein Punkt
ist die Zielvariable oder Klasse ist eine spezifische Klasse, die annehmen kann ist die Merkmalsvariable ist der spezifische Wert der Merkmalsvariable ist die Anzahl der nächsten Nachbarn ist die Menge der nächsten Nachbarn von ist eine Indikatorfunktion, die 1 ist, wenn , und 0 sonst
Standardfehler in der linearen Regression
wie sieht der standard fehler aus in der regression?
?
Die Formeln für die Standardfehler der Koeffizienten (\beta_0) und (\beta_1) in der linearen Regression lauten:
- (\sigma^2): Varianz der Fehlerterme
- (n): Anzahl der Beobachtungen
- (\bar{x}): Mittelwert der Prädiktorwerte
- (x_i): Einzelne Prädiktorwerte
Annahmen:
- Unabhängige Stichproben
- Normalverteilung der Fehler
- Konstante Varianz der Fehler (Homoskedastizität)
Was ist das RSS
?
Die Residual Sum of Squares (RSS) ist eine Metrik, die verwendet wird, um die Abweichung der vorhergesagten Werte von den tatsächlichen Werten in einem linearen Regressionsmodell zu messen. Sie summiert die quadrierten Residuen, die die Differenzen zwischen den beobachteten und den vorhergesagten Werten darstellen.
oder äquivalent
ist die Vorhersage für basierend auf dem -ten Wert von ist das -te Residuum ist die Residual Sum of Squares ist der beobachtete Wert ist der geschätzte Achsenabschnitt ist der geschätzte Koeffizient für ist der -te Wert von
Warum quadratische Fehler Therme bei der Linearen Regression
?
Die lineare Regression ist ein statistisches Verfahren, das verwendet wird, um die Beziehung zwischen einer abhängigen Variablen
ist die abhängige Variable ist der Achsenabschnitt (Intercept) des Modells ist der Koeffizient für die unabhängige Variable ist die unabhängige Variable ist der Fehlerterm, der die Residuen darstellt
Die Fehlerterme
bedeutet, dass die Fehler normalverteilt sind mit einem Mittelwert von 0 und einer Varianz von
Die Residuen
ist das Residuum für die -te Beobachtung ist der beobachtete Wert für die -te Beobachtung ist der vorhergesagte Wert für die -te Beobachtung
Welche Annahmen macht die Lineare Regression
?
Die lineare Regression basiert auf mehreren grundlegenden Annahmen, die sicherstellen, dass die Schätzungen der Regressionskoeffizienten unverzerrt und effizient sind, und dass die Inferenzstatistik gültig ist.
-
Linearität:
- Die Beziehung zwischen der unabhängigen Variable (X) und der abhängigen Variable (Y) ist linear. Das bedeutet, dass (Y) als eine lineare Funktion von (X) beschrieben werden kann.
-
Unabhängigkeit der Fehler:
- Die Fehlerterme (\epsilon) sind voneinander unabhängig. Das bedeutet, dass der Fehlerterm einer Beobachtung keine Informationen über den Fehlerterm einer anderen Beobachtung liefert.
-
Homoskedastizität:
- Die Varianz der Fehlerterme (\epsilon) ist konstant über alle Werte von (X). Das bedeutet, dass die Streuung der Fehler über den Bereich der unabhängigen Variablen gleich bleibt.
-
Normalverteilung der Fehler:
- Die Fehlerterme (\epsilon) sind normalverteilt mit einem Mittelwert von 0 und einer Varianz von (\sigma^2).
-
Keine perfekte Multikollinearität (für multiple lineare Regression):
- Keine der unabhängigen Variablen ist eine perfekte lineare Funktion einer anderen. Dies stellt sicher, dass die Koeffizienten der Regression eindeutig bestimmt werden können.
-
Exogenität:
- Die unabhängigen Variablen sind nicht korreliert mit den Fehlertermen. Das bedeutet, dass die erklärenden Variablen nicht systematisch mit den Störgrößen zusammenhängen.
Was ist die Maximum Likelihood Schaetzung bei der Linearen Regression? (Herleitung Least Squares)
?
Die Maximum-Likelihood-Schätzung (MLE) ist eine Methode zur Schätzung der Parameter eines statistischen Modells. In der linearen Regression wird MLE verwendet, um die Koeffizienten zu finden, die die Wahrscheinlichkeit der beobachteten Daten maximieren.
Die Wahrscheinlichkeit der Beobachtungen gegeben die Parameter
Dies kann vereinfacht werden zu:
Um die MLE zu berechnen, maximieren wir das Log-Likelihood:
Da der erste Term eine Konstante ist, können wir ihn ignorieren:
ist die abhängige Variable ist die unabhängige Variable ist der Achsenabschnitt (Intercept) des Modells ist der Koeffizient für die unabhängige Variable ist der beobachtete Wert für die -te Beobachtung ist der vorhergesagte Wert für die -te Beobachtung ist der Fehlerterm, der die Residuen darstellt ist die Varianz des Fehlerterms
Warum funktioniert die Herleitung der Least Squares?
?
Weil man die Normalverteilung annimmt und somit die Maximum Likelihood wie bereits daargelegt. Die Logitische Regression laesst sich auch einfach als Maximum likelihood Problem formulieren und loesen.
Standard Error of the Coefficient Estimates
Wie wird das Konfidenzintervall aufgestellt?
?
Standardfehler der Koeffizientenschätzungen:
Der Standardfehler gibt an, wie die Schätzung bei wiederholter Stichprobenziehung variiert.
wobei
Konfidenzintervalle:
Ein 95%-Konfidenzintervall für
Dieses Intervall enthält den wahren Wert von
: Varianz der Fehlerterme : Anzahl der Beobachtungen : Mittelwert der Prädiktorwerte : Einzelne Prädiktorwerte : Standardfehler : Interzept des Modells : Koeffizient für den Prädiktor
Hypothesen Tests in Linearer Regression
?
In der linearen Regression wird häufig ein Hypothesentest verwendet, um zu überprüfen, ob eine Beziehung zwischen der unabhängigen Variable
Die Nullhypothese (
versus die Alternativhypothese
Mathematisch entspricht dies dem Testen der folgenden Hypothesen:
versus
ist die Nullhypothese, die besagt, dass der Koeffizient gleich null ist, was bedeutet, dass keine lineare Beziehung zwischen und besteht. ist die Alternativhypothese, die besagt, dass der Koeffizient ungleich null ist, was bedeutet, dass eine lineare Beziehung zwischen und besteht.
Wenn
Dies würde bedeuten, dass
Um die Hypothese zu testen, verwenden wir den t-Test, der wie folgt definiert ist:
Hierbei ist:
der geschätzte Koeffizient für die unabhängige Variable der Standardfehler von
Der t-Wert gibt an, wie viele Standardabweichungen der geschätzte Koeffizient von der Nullhypothese abweicht. Ein großer absoluter Wert von
Z-Score im Vergleich zum t-Score:
- Der t-Score wird verwendet, wenn die Stichprobengröße klein ist (normalerweise
) und/oder die Populationsvarianz unbekannt ist. Er folgt der t-Verteilung. - Der Z-Score wird verwendet, wenn die Stichprobengröße groß ist (normalerweise
) und die Populationsvarianz bekannt ist. Er folgt der Standardnormalverteilung (Normalverteilung mit Mittelwert 0 und Varianz 1).
Wie ist der RSE?
?
Der Residual Standard Error (RSE) ist ein Schätzwert für die Standardabweichung des Fehlerterms
Der RSE wird mit der folgenden Formel berechnet:
wobei:
die Anzahl der Beobachtungen ist die Residual Sum of Squares ist der beobachtete Wert der -ten Beobachtung ist der vorhergesagte Wert der -ten Beobachtung ist
Die RSS (Residual Sum of Squares) ist definiert als:
Der RSE schätzt die durchschnittliche Abweichung der beobachteten Werte von den vorhergesagten Werten, wenn das Modell die wahre Beziehung zwischen den Variablen perfekt beschreiben würde.
ist die Anzahl der Beobachtungen ist die Residual Sum of Squares ist der beobachtete Wert der -ten Beobachtung ist der vorhergesagte Wert der -ten Beobachtung
Hypothesentest in der linearen Regression
Wie sieht der t test aus?
?
Um die Nullhypothese zu testen, berechnen wir die t-Statistik:
Diese folgt einer t-Verteilung mit ( n - 2 ) Freiheitsgraden, unter der Annahme, dass ( \beta_1 = 0 ) ist.
Mit statistischer Software lässt sich die Wahrscheinlichkeit berechnen, einen Wert gleich oder größer als (|t|) zu beobachten. Diese Wahrscheinlichkeit nennt man den p-Wert.
: Geschätzter Koeffizient : Standardfehler des geschätzten Koeffizienten : Anzahl der Beobachtungen : t-Statistik
Welche Verteilung braucht welches Modell der Regression?
?
GLM
Warum ist der
?
Weil mit mehr Variblen, Parameter desto besser wird der
Was ist die F-Statistic?
?
In der multiplen linearen Regression wird die F-Statistik verwendet, um zu überprüfen, ob alle Regressionskoeffizienten gleich null sind, also ob das Modell signifikant zur Erklärung der Varianz der abhängigen Variablen beiträgt.
Die Nullhypothese (
versus
ist die Nullhypothese, die besagt, dass alle Regressionskoeffizienten gleich null sind, was bedeutet, dass die unabhängigen Variablen keinen Einfluss auf die abhängige Variable haben. ist die Alternativhypothese, die besagt, dass mindestens ein Regressionskoeffizient ungleich null ist, was bedeutet, dass mindestens eine unabhängige Variable einen Einfluss auf die abhängige Variable hat.
Dieser Hypothesentest wird durch Berechnung der F-Statistik durchgeführt:
wobei:
(Total Sum of Squares) die totale Quadratsumme ist und berechnet wird als:
(Residual Sum of Squares) die Residualquadratsumme ist und berechnet wird als:
die Anzahl der Prädiktoren ist die Anzahl der Beobachtungen ist
Die F-Statistik vergleicht das Modell mit allen Prädiktoren gegen ein Modell ohne Prädiktoren. Ein hoher F-Wert deutet darauf hin, dass das Modell einen signifikanten Teil der Varianz der abhängigen Variablen erklärt.
Wie werden Categoriale Variablen umcodiert?
?
In diesem Beispiel verwenden wir eine binäre Variable als Prädiktor in der Regressionsgleichung. Das resultierende Modell ist:
kann als der durchschnittliche Wert von interpretiert werden, wenn . kann als der durchschnittliche Wert von interpretiert werden, wenn . ist der durchschnittliche Unterschied im Wert von zwischen den Gruppen und .
Die Schätzungen der Koeffizienten und andere Informationen, die mit dem Modell verbunden sind, liefern wichtige Einblicke in die Beziehung zwischen der binären Prädiktorvariablen und der Zielvariablen
Beispielhafte Interpretationen könnten sein:
- Der durchschnittliche Wert von
für die Gruppe mit . - Der durchschnittliche Wert von
für die Gruppe mit . - Der Unterschied im durchschnittlichen Wert von
zwischen den beiden Gruppen.
Was stellt eine Interaktion dar in der Regression zwischen Dummy Variablen?
?
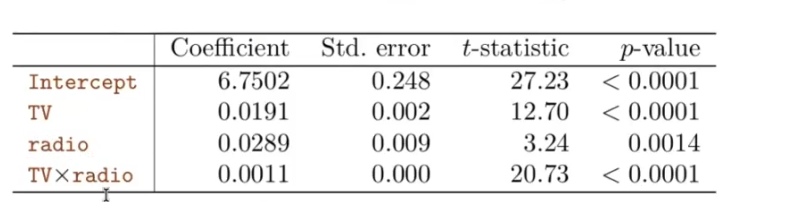
In der linearen Regression können Dummy-Variablen verwendet werden, um kategoriale Prädiktoren darzustellen. Wenn Interaktionen zwischen Dummy-Variablen einbezogen werden, ermöglicht dies die Untersuchung der kombinierten Effekte dieser Variablen auf die Zielvariable
Betrachten wir folgendes Modell:
Hierbei sind
: Der durchschnittliche Wert von , wenn und . : Die Veränderung des durchschnittlichen Werts von , wenn von 0 auf 1 wechselt, während konstant bleibt. : Die Veränderung des durchschnittlichen Werts von , wenn von 0 auf 1 wechselt, während konstant bleibt. : Der Interaktionseffekt zwischen und . Dies ist die zusätzliche Veränderung im durchschnittlichen Wert von , wenn sowohl als auch von 0 auf 1 wechseln, im Vergleich zur Summe der einzelnen Effekte von und .
Das Modell kann die folgenden Szenarien erklären:
-
Beide Dummy-Variablen sind 0 (
, ): Dies ist der Grundwert (Referenzkategorie).
-
Nur
ist 1 ( , ): Der Effekt von
alleine. -
Nur
ist 1 ( , ): Der Effekt von
alleine. -
Beide Dummy-Variablen sind 1 (
, ): Der kombinierte Effekt von
und sowie deren Interaktion.
Die Interaktionsterm
Wie veraendert sich der Plot mit Interaction in der Regression?
?
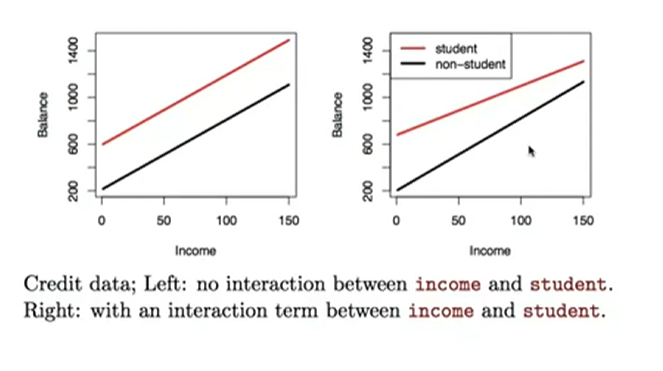
Was kann passieren wenn man nun zuviele Dummy Variablen hat?
?
Betrachten wir das folgende lineare Regressionsmodell mit Dummy-Variablen:
In diesem Modell:
, wenn die Person aus dem Süden kommt, und sonst. , wenn die Person aus dem Westen kommt, und sonst. - Die Referenzkategorie (Osten) ist durch das Fehlen beider Dummy-Variablen (
und ) dargestellt.
Problem der linearen Abhängigkeit:
Wenn wir eine weitere Dummy-Variable
, wenn die Person aus dem Norden kommt, und sonst.
Dies würde das Modell folgendermaßen ändern:
Da jede Person aus dem Süden, Westen, Osten oder Norden kommen muss, würden die Dummy-Variablen
Hierbei ist
Diese lineare Abhängigkeit führt zu Multikollinearität, was bedeutet, dass die Design-Matrix nicht mehr invertierbar ist und die Regressionskoeffizienten
Um dieses Problem zu vermeiden, sollte man nur
Sprich was muss man bei Dummy Variablen machen, um Multikolineraitaet zu vermeiden?
?
Ein
Was nennt man eine Interaction?
?
Man Multipliziert die Dummies gegenseitig miteinander
 beispiel: The model equation would be:
beispiel: The model equation would be:
Welche Probleme gibt es bei der Regression?
?

Wie kann man nicht linearitaet mit einem Linearen Model modelieren?
?
Nichtlineare Beziehungen zwischen Variablen können in einem linearen Regressionsmodell dargestellt werden, indem nichtlineare Terme der unabhängigen Variablen hinzugefügt werden. Ein Beispiel ist die Hinzufügung eines quadratischen Terms:
Betrachten wir das folgende Modell:
Hierbei:
ist der Achsenabschnitt (Intercept) des Modells. ist der Koeffizient für den linearen Term der unabhängigen Variable "horsepower". ist der Koeffizient für den quadratischen Term der unabhängigen Variable "horsepower". ist der Fehlerterm.
Obwohl das Modell einen quadratischen Term enthält, bleibt es ein lineares Modell, weil die Koeffizienten (
Vorteile der Hinzufügung quadratischer Merkmale:
-
Erfassen von Nichtlinearitäten: Das Modell kann die nichtlineare Beziehung zwischen "horsepower" und "mpg" besser erfassen, da es den Effekt von "horsepower" sowohl linear als auch quadratisch berücksichtigt.
-
Flexibilität: Durch das Hinzufügen von Polynomtermen (z.B. quadratische, kubische) kann das Modell flexibler gestaltet werden, um komplexere Beziehungen zu modellieren.
Beispielhafte Interpretation:
- Der Koeffizient
beschreibt die Änderung in "mpg" für eine Einheit Änderung in "horsepower", wenn alle anderen Terme konstant gehalten werden. - Der Koeffizient
beschreibt den zusätzlichen Effekt, der auftritt, wenn "horsepower" quadratisch zunimmt.
Zusammengefasst: Durch das Hinzufügen von nichtlinearen Termen wie
Lineares Modell:
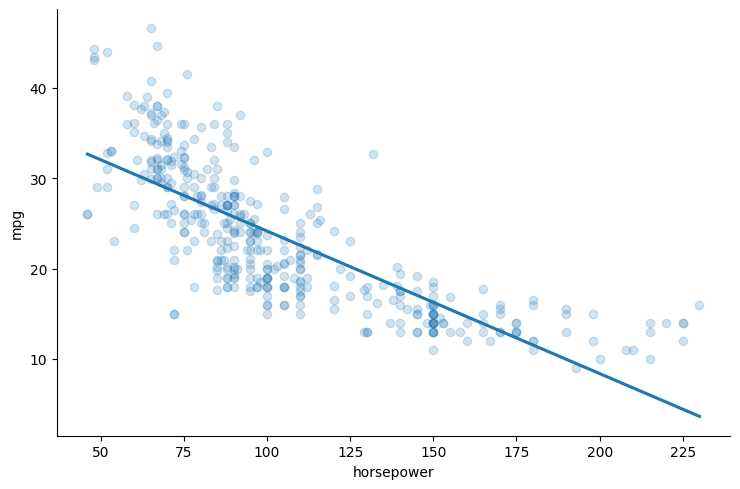
Quadratisches Modell mit quadratischem Term:
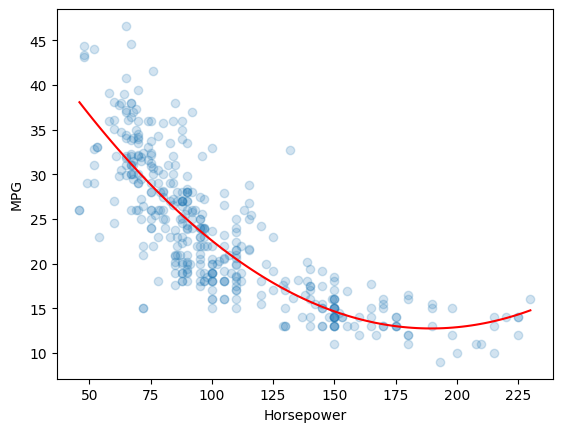
Was ist nicht linearität
?
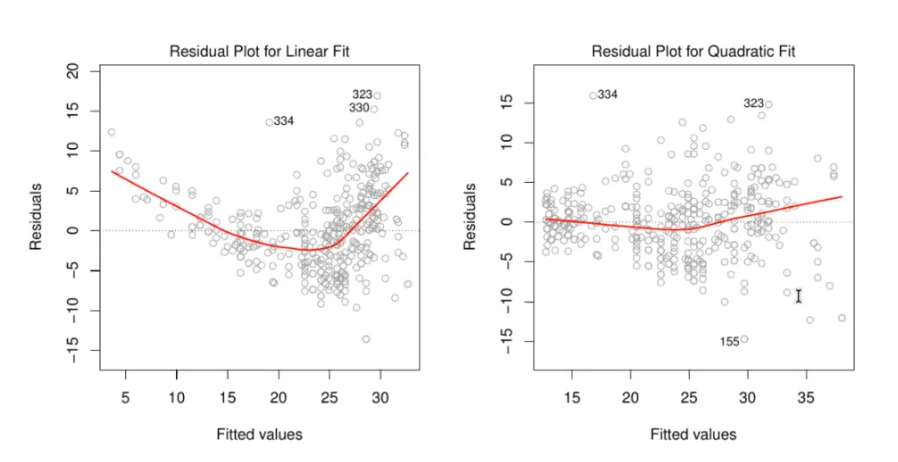
Hier sieht man, dass der erste Plot einen Trendaufweist, dies sollte nicht sein, eventuell transformieren mit wurzel quadrat oder log. Dies sieht man am besten mit Residuen Plots.
Was ist das Problem mit der Korrelation der Fehler Thermen
?
todo
Was ist heterogestatisch?
?
Der Begriff "heteroskedastisch" bezieht sich auf eine Situation in der Regressionsanalyse, bei der die Varianz der Fehlerterme ((\epsilon)) nicht konstant ist über die Beobachtungen hinweg. Dies steht im Gegensatz zur Annahme der Homoskedastizität, bei der die Varianz der Fehler konstant bleibt.
Heteroskedastizität
Definition: Heteroskedastizität liegt vor, wenn die Varianz der Störgrößen ((\epsilon)) in einem Regressionsmodell nicht konstant ist, sondern von den Werten der unabhängigen Variablen abhängt.
Formel: Es gibt keine spezifische Formel für Heteroskedastizität, aber es betrifft die Varianz der Fehlerterme:
- (\epsilon_i): Fehlerterm für die (i)-te Beobachtung
- (\sigma_i^2): Varianz des Fehlerterms, die von (i) abhängt
Konsequenzen: Heteroskedastizität kann zu ineffizienten und verzerrten Schätzungen der Regressionskoeffizienten führen, da die Annahme der konstanten Varianz verletzt wird.
Erkennung: Heteroskedastizität kann durch visuelle Inspektion von Residuenplots oder statistische Tests wie den Breusch-Pagan-Test oder den White-Test identifiziert werden.
Behandlung: Es gibt mehrere Methoden, um Heteroskedastizität zu behandeln, einschließlich der Verwendung von robusten Standardfehlern, Transformation der Daten (z.B. Log-Transformation), oder gewichtete kleinste Quadrate (WLS).
Was ist Homoskedastizität ::
Was machst du hier: 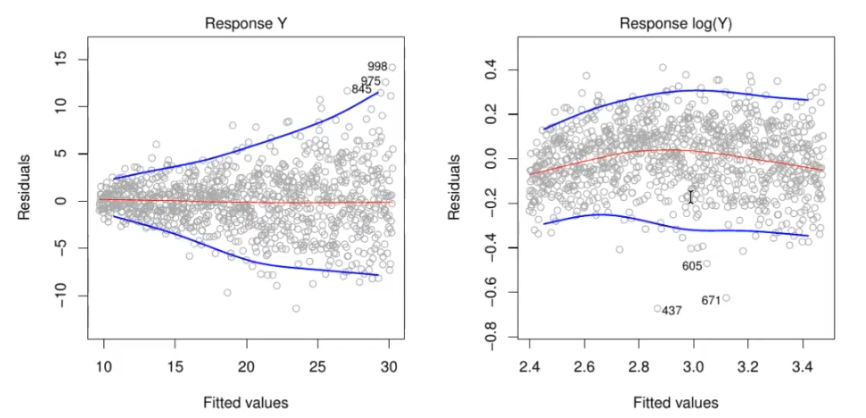 ?
?
Logartymus
\
Was ist ein Aussreiser
?
Art1 (Ist in der Verteilung von X drin) sprich nicht so gut aber auch nicht so schlimm --> schadet der Evaluiereung : 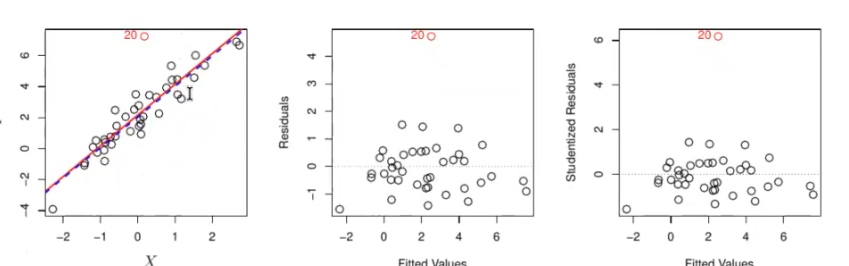 Art2 (high Leverage Outliers) --> Schadet dem Model und der Evaluierung:
Art2 (high Leverage Outliers) --> Schadet dem Model und der Evaluierung: 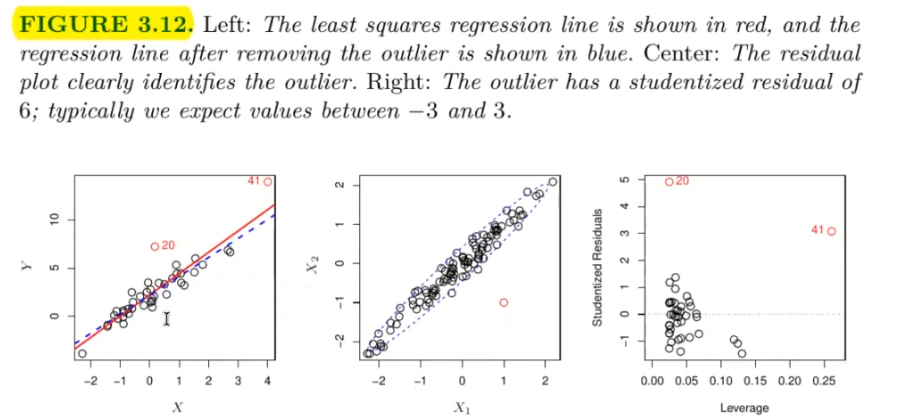
Wie kann man high Leverage Points erkennen?
?
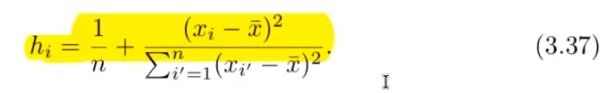
Was ist koolinerität?
?
todo
Was ist multikoolinerität
?
todo
Wie bemerkt man multikolinerität?
?
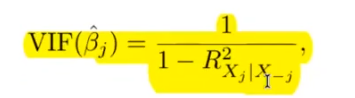 je grösser der VIF desto eher hat man eine Kolinerität.
je grösser der VIF desto eher hat man eine Kolinerität.
Maßnahmen bei Multikollinearität
Massnahmen bei Multikolinerität
?
Multikollinearität tritt auf, wenn zwei oder mehr Prädiktoren in einem Regressionsmodell stark korreliert sind, was zu instabilen Schätzungen der Regressionskoeffizienten führt. Hier sind einige Maßnahmen, um Multikollinearität zu adressieren:
1. Prädiktoren entfernen:
- Entfernen hoch korrelierter Prädiktoren, um die Modellstabilität zu verbessern.
2. Hauptkomponentenanalyse (PCA):
- Reduziert die Dimensionen der Daten, indem sie die Daten auf unkorrelierte Hauptkomponenten projiziert.
3. Regularisierungsmethoden:
- Ridge Regression und Lasso Regression können verwendet werden, um die Auswirkungen von Multikollinearität zu verringern.
4. Datenzentrierung und -skalierung:
- Zentrieren und skalieren der Prädiktoren, um die Multikollinearität zu reduzieren.
(R^2) und Restquadratsumme
wie berechnet man r2?
?
Restquadratsumme (RSS):
Totalquadratsumme (TSS):
Bestimmtheitsmaß ((R^2)):
(R^2) misst den Anteil der Gesamtvarianz, der durch das Modell erklärt wird.
- (\text{RSS}): Restquadratsumme
- (\text{TSS}): Totalquadratsumme
- (y_i): Beobachteter Wert
- (\hat{y}_i): Vorhergesagter Wert
- (\bar{y}): Mittelwert der beobachteten Werte
- (n): Anzahl der Beobachtungen
Classification
Warum benutzt man Logistic Regression und nicht Linreg?
?
- weil negative values
- und nicht zwischen 1 und 0
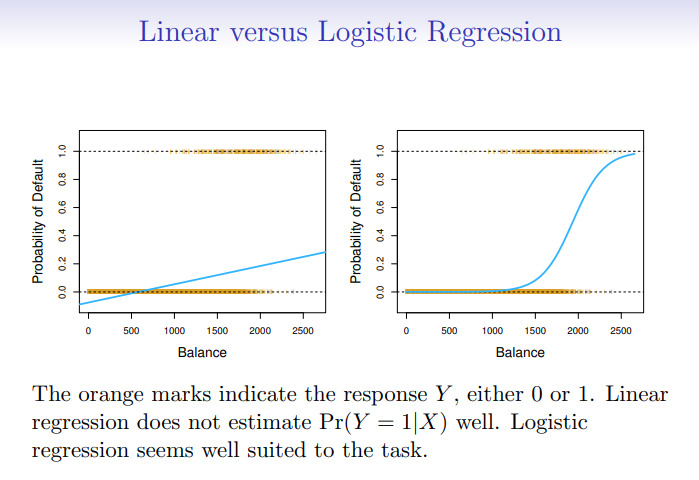
Was ist das Discison boundrie?
?
Eine Decision Boundary ist eine Grenze im Merkmalsraum, die verschiedene Klassen in einem Klassifikationsproblem voneinander trennt. Sie wird durch ein Klassifikationsmodell definiert und trennt Regionen, in denen verschiedene Klassen dominieren.
- In linearen Modellen (z.B. Logistic Regression) ist die Decision Boundary eine lineare Trennlinie.
- In nichtlinearen Modellen (z.B. Support Vector Machines mit Kerneln) kann die Decision Boundary komplexe Formen annehmen.
Eine Decision Boundary kann durch visuelle Darstellung der Klassen im Merkmalsraum veranschaulicht werden.
Was ist der Threshhold in Logistic Regression ::
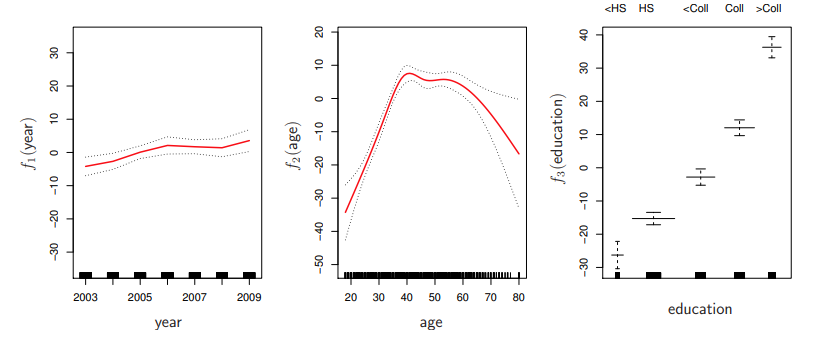
Formel für die Logistische Regression
?
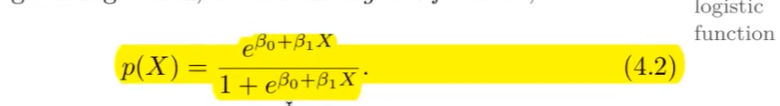 output: Zahl zwischen 0 und 1 muss nicht die Wahrscheinlichkeit sein.
output: Zahl zwischen 0 und 1 muss nicht die Wahrscheinlichkeit sein.
Formel Logistische Regression Odss umstellung
?
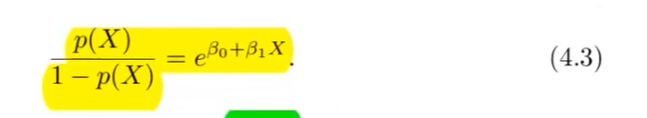
output: Odds
Formel Odds mit Logartymuss
?
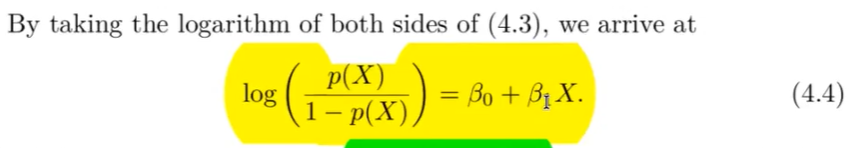
Maximum Likelihood
Wie sieht die Maximum likelihood aus von der logistischen Regression?
?
Maximum-Likelihood-Schätzung wird verwendet, um die Parameter zu schätzen. Die Likelihood-Funktion für die logistische Regression lautet:
Diese Likelihood gibt die Wahrscheinlichkeit der beobachteten Nullen und Einsen in den Daten an. Wir wählen
: Interzept : Koeffizient für die Variable : Wahrscheinlichkeitsvorhersage für Beobachtung (i) : Beobachteter Wert
In R kann das Modell mit der glm-Funktion angepasst werden.
Beispiel Logistische Regression?
?

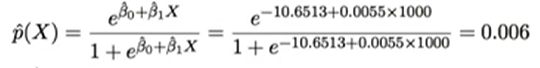
Logistische Regression mit dummy variblen binaer
?

Multinominal Logistic Regression
was ist Multinominale Logistic Regression?
?
mehrere Klassen:

Z-Statistic
?
Die Z-Statistic misst, wie viele Standardabweichungen ein Datenpunkt vom Mittelwert entfernt ist. Sie wird verwendet, um Hypothesentests durchzuführen und zu bestimmen, ob ein Datenpunkt signifikant von einem erwarteten Wert abweicht.
- ( X ): Beobachteter Wert
- ( \mu ): Erwartungswert
- ( \sigma ): Standardabweichung
Bernoulli-Verteilung
Wie ist die Bernoulli Verteilung?
?
Die Bernoulli-Verteilung modelliert einen binären Ausgang (Erfolg oder Misserfolg) mit einer Wahrscheinlichkeit ( p ) für Erfolg und ( 1-p ) für Misserfolg.
Varianz der Bernoulli-Verteilung:
Die Varianz kann berechnet werden, da sie die Streuung der binären Ausgänge um den Mittelwert ( p ) misst:
- ( p ): Wahrscheinlichkeit für Erfolg
- ( 1-p ): Wahrscheinlichkeit für Misserfolg
Diese Berechnung ist möglich, weil die Varianz der Bernoulli-Verteilung die Wahrscheinlichkeit berücksichtigt, dass ein Ausgang von der Erwartung ( p ) abweicht.
T-Statistic in Linearer Regression
Der T-Statistic wird in der linearen Regression verwendet, um die Signifikanz eines einzelnen Regressionskoeffizienten zu testen. Da die Varianz des Fehlerterms (\sigma^2) unbekannt ist, muss sie aus den Daten geschätzt werden.
Die Formel für die T-Statistic lautet:
: Geschätzter Koeffizient für den (j)-ten Prädiktor : Standardfehler des geschätzten Koeffizienten - Diese Teststatistik folgt unter der Nullhypothese einer t-Verteilung mit (n - p - 1) Freiheitsgraden, wobei (n) die Anzahl der Beobachtungen und (p) die Anzahl der Prädiktoren ist.
Modelle können nur Korrelation erklären was jedoch nicht :: Kausalzusammenhänge --> Confounding
Was ist die Multinominale Logitische Regression :: Regression mit mehrern Klassen
Wie sieht die Formel für die Multinominale Regression aus?
?
Sprich Softmax --> Alle Summieren sich auf 1
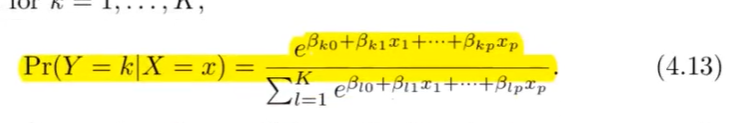
Formel für Odds mit mit baseline comparative
?
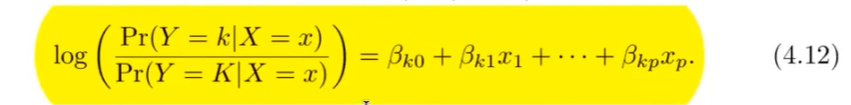
Hier sind die wichtigsten Konzepte und Formeln von der angegebenen Webseite im Stil der bisherigen Erklärungen:
Wie sieht die Formel der Logistischen Regression aus
?
Logistic Regression modelt die Wahrscheinlichkeit, dass die Antwortvariable ( Y ) einer bestimmten Kategorie angehört. Das Modell wird wie folgt ausgedrückt:
Dies kann in die Logit-Funktion umgeschrieben werden:
: Interzept : Koeffizient für den Prädiktor ( X )
Was ist die Maximum Liklihood verfahren?
?
Die Koeffizienten werden durch das Maximum-Likelihood-Verfahren geschätzt, das versucht,
Um zu überprüfen, ob ein Zusammenhang zwischen der Wahrscheinlichkeit einer Klasse und einem Prädiktor besteht, wird ein Hypothesentest durchgeführt:
- ( z )-statistic misst die Anzahl der Standardabweichungen, die ( \beta_1 ) von 0 entfernt ist.
Wie sieht die Mulltiple Lineare Regression aus?
?
Wenn mehrere Prädiktoren vorhanden sind, wird das Modell wie folgt erweitert:
- Die Interpretation der Koeffizienten bleibt ähnlich, wobei die Werte der anderen Prädiktoren konstant gehalten werden.
LDA modelliert die Verteilungen der Prädiktoren in jeder Antwortklasse und verwendet den Satz von Bayes, um diese in Schätzungen zu überführen:
- (
): A-priori-Wahrscheinlichkeit für Klasse ( k ) - (
): Dichtefunktion der Prädiktoren für Klasse ( k )
Logistic Regression vs. LDA
wann lda wann logistische regression?
Für ein Zwei-Klassen-Problem kann gezeigt werden, dass für LDA:
Dies hat die gleiche Form wie die logistische Regression. Der Unterschied liegt in der Schätzung der Parameter.
Logistische Regression:
- Nutzt die bedingte Likelihood basierend auf
(bekannt als diskriminatives Lernen).
LDA:
- Nutzt die vollständige Likelihood basierend auf
(bekannt als generatives Lernen).
Trotz dieser Unterschiede sind die Ergebnisse in der Praxis oft sehr ähnlich.
: Wahrscheinlichkeit, dass die Beobachtung (x) zu Klasse 1 gehört : Wahrscheinlichkeit, dass die Beobachtung (x) zu Klasse 2 gehört : Koeffizienten der linearen Kombination der Prädiktoren : Prädiktoren
Bayes-Theorem für Klassifikation
Was ist die LDA Linear Discriminant analysis?
?
Thomas Bayes war ein Mathematiker, dessen Theorem ein bedeutender Teilbereich der Statistik und probabilistischen Modellierung ist. Das Bayes-Theorem wird für die Klassifikation wie folgt verwendet:
Für die Diskriminanzanalyse wird es leicht abgewandelt:
: Zufallsvariable der Klasse : Spezifische Klasse : Eingabevektor : Spezifische Beobachtung von : Gesamtzahl der Klassen : A-priori-Wahrscheinlichkeit für Klasse : Dichtefunktion für in Klasse : Posteriori-Wahrscheinlichkeit für Klasse gegeben : Likelihood von gegeben Klasse : A-priori-Wahrscheinlichkeit für Klasse : Gesamtwahrscheinlichkeit von
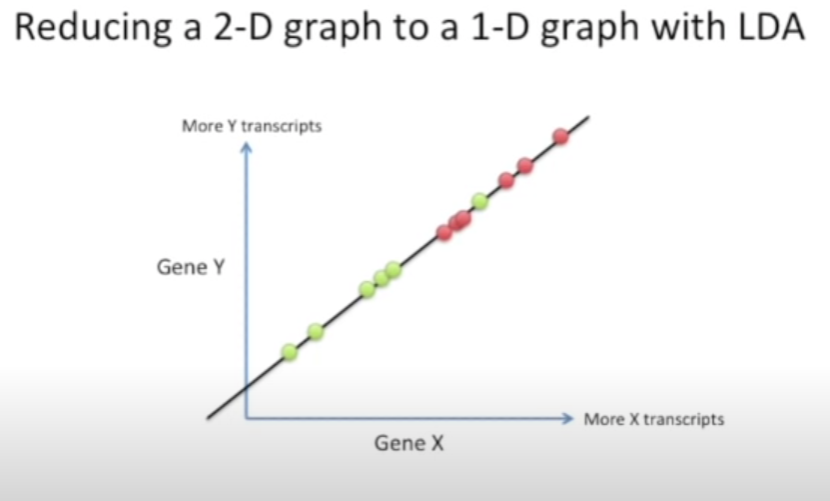
was macht LDA genau?
?
LDA macht eine Dimensions Reduzierung aehnlich zu PCA. Es projeziert jedoch nicht die Punkte, sondern macht einen neuen Space und Projeziert dann die Punkte auf diesen Space. LDA erstellt eine neue Axe die die Distanz der durchschnittlichen distance zwischen zwei categorien minizmiert.
QDA lockert die Annahme einer gemeinsamen Kovarianzmatrix und erlaubt jede Klasse ihre eigene Kovarianzmatrix zu haben, was es flexibler macht, aber auch zu höherer Varianz führt.
KNN klassifiziert Beobachtungen basierend auf den ( K ) nächsten Nachbarn:
- Die Wahl von ( K ) beeinflusst die Flexibilität und Bias-Varianz-Abwägung des Modells.
Wann LDA und wann QDA verwenden
Wann soll man LDA verwenden anstatt Log reg?
?
LDA (Linear Discriminant Analysis):
- Verwenden, wenn die Kovarianzmatrizen der Klassen ungefähr gleich sind.
- Geeignet für große Datensätze mit vielen Beobachtungen pro Klasse.
- Stabiler bei kleineren Datensätzen.
QDA (Quadratic Discriminant Analysis):
- Verwenden, wenn die Kovarianzmatrizen der Klassen unterschiedlich sind.
- Nützlich für komplexere Modelle mit größeren Unterschieden zwischen den Klassen.
- Erfordert größere Datensätze, da es mehr Parameter schätzt.
Logistische Regression:
- Verwenden, wenn eine lineare Entscheidungsgrenze erwartet wird.
- Flexibler als LDA bei kleineren Datensätzen und weniger Annahmen über die Verteilung der Prädiktoren.
- Wird nicht verwendet, wenn die Daten nicht gut durch eine lineare Entscheidungsgrenze getrennt werden können.
Generative Models for Classification
Wie sehen Gernerative Modelle aus?
?

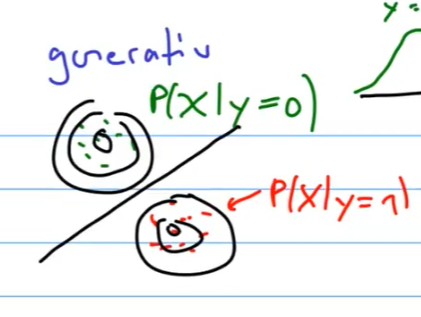
LDA (verwenden bei weniger Daten)
Linear Discriminant Analysis (LDA)
wie sieht LDA aus?
?
LDA ist eine Methode zur Klassifizierung, die die Varianz zwischen den Klassen maximiert und die Varianz innerhalb der Klassen minimiert. Die Entscheidungsregel basiert auf der größten diskriminanten Funktion ( \delta_k(x) ):
: Eingabevektor : Gemeinsame Kovarianzmatrix : Mittelwert der Klasse ( k ) : A-priori-Wahrscheinlichkeit der Klasse ( k )
Quadratic Discriminant Analysis (QDA)
Wie sieht QDA aus?
?
QDA ist eine Erweiterung von LDA, bei der jede Klasse ihre eigene Kovarianzmatrix hat. Die Entscheidungsregel basiert auf der größten diskriminanten Funktion ( \delta_k(x) ):
- ( x ): Eingabevektor
- ( \Sigma_k ): Kovarianzmatrix der Klasse ( k )
- ( \mu_k ): Mittelwert der Klasse ( k )
- ( \pi_k ): A-priori-Wahrscheinlichkeit der Klasse ( k )
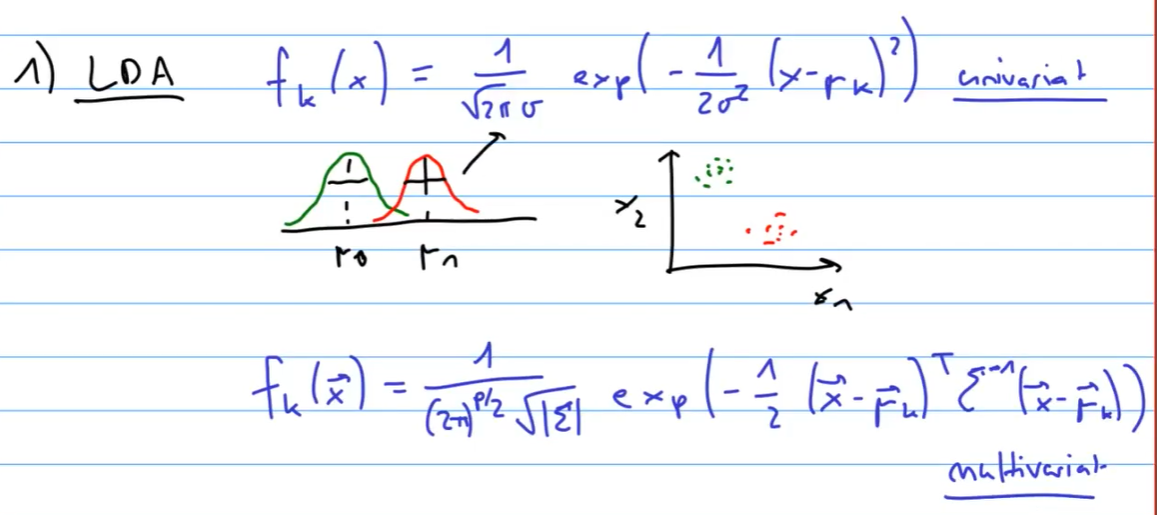
Was ist LDA und wie ist die Formel
?

Univariater Fall:
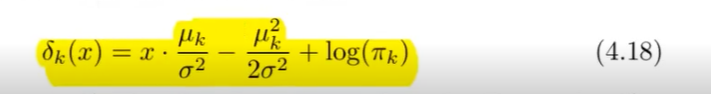
Multivariater Fall:
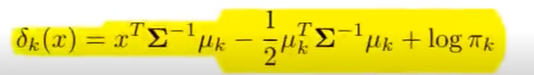
QDA (verwenden bei vielen Daten)

Naive bayes NB (multivariat)

Wie werden die Optimalen Betas in Logistischer Regression berechnen? :: Maximum Likelihood
Wie werden die Optimalen Betas in LDA berechnet? :: Wir passen eine Normalverteilung an unsere Daten an.
Performance Messung bei Binärklassifikation
Confusion Matrix:
Accuracy
Wie ist die Formel fuer die Accuracy?
?
Accuracy ist der Anteil der korrekten Vorhersagen:
Sensitivity / Recall
Was ist Sensitity / Recall?
?
Sensitivity (auch Recall genannt) ist ein Maß dafür, wie gut ein Modell tatsächlich positive Fälle korrekt identifiziert. Es ist der Anteil der tatsächlich positiven Fälle, die vom Modell korrekt als positiv klassifiziert wurden.
Die Formel für Sensitivity / Recall lautet:
- ( TP ): True Positives (Anzahl der korrekt als positiv klassifizierten positiven Fälle)
- ( FN ): False Negatives (Anzahl der tatsächlich positiven, aber als negativ klassifizierten Fälle)
Ein hoher Recall-Wert bedeutet, dass das Modell nur wenige tatsächliche positive Fälle übersieht.
Precision
Was ist die Precison?
?
Precision ist ein Maß dafür, wie viele der als positiv klassifizierten Fälle tatsächlich positiv sind. Es ist der Anteil der korrekt vorhergesagten positiven Fälle an allen vorhergesagten positiven Fällen.
Die Formel für Precision lautet:
- ( TP ): True Positives (Anzahl der korrekt als positiv klassifizierten positiven Fälle)
- ( FP ): False Positives (Anzahl der fälschlicherweise als positiv klassifizierten negativen Fälle)
Ein hoher Precision-Wert bedeutet, dass das Modell nur wenige negative Fälle fälschlicherweise als positiv klassifiziert. dass das Modell nur wenige tatsächliche positive Fälle übersieht.
Specificity
Was sagt die Specifity aus?
?
Specificity misst, wie gut ein Modell tatsächlich negative Fälle korrekt identifiziert. Es ist der Anteil der tatsächlich negativen Fälle, die vom Modell korrekt als negativ klassifiziert wurden.
Die Formel für Specificity lautet:
- ( TN ): True Negatives (Anzahl der korrekt als negativ klassifizierten negativen Fälle)
- ( FP ): False Positives (Anzahl der fälschlicherweise als positiv klassifizierten negativen Fälle)
Ein hoher Specificity-Wert bedeutet, dass das Modell nur wenige tatsächliche negative Fälle fälschlicherweise als positiv klassifiziert.
Trade-off zwischen Specificity, Recall und Precision
Erklaere den Trade off zwischen Specifity recall und Precision?
?
Specificity, Recall und Precision sind wichtige Maße für die Leistungsfähigkeit eines Klassifikationsmodells. Änderungen in einem Maß können oft zu Kompromissen in den anderen führen:
- Recall vs. Precision: Ein hohes Recall führt oft zu einem niedrigeren Precision, da mehr positive Vorhersagen gemacht werden, was auch die False Positives erhöht. Umgekehrt führt ein hohes Precision oft zu einem niedrigeren Recall.
- Recall vs. Specificity: Ein hohes Recall bedeutet, dass mehr tatsächliche Positive erkannt werden, was die Anzahl der False Negatives verringert, aber die Anzahl der False Positives erhöhen kann, was die Specificity verringert.
- Specificity vs. Precision: Ein hohes Specificity bedeutet, dass viele tatsächliche Negative korrekt erkannt werden, was die Anzahl der False Positives verringert und somit Precision erhöht.
Decision Threshold
Erklaere den Descision Threshold
?
Der Decision Threshold ist der Schwellenwert, ab dem eine Beobachtung als positiv klassifiziert wird. Durch Anpassen des Decision Threshold kann man den Trade-off zwischen Recall, Precision und Specificity steuern:
- Niedriger Threshold: Erhöht Recall, verringert Specificity und Precision.
- Hoher Threshold: Erhöht Specificity und Precision, verringert Recall.
- Die Wahl des geeigneten Decision Threshold hängt von den spezifischen Anforderungen und Prioritäten der Anwendung ab.
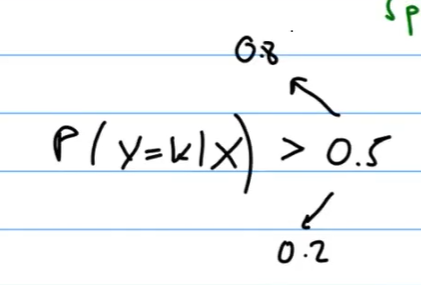
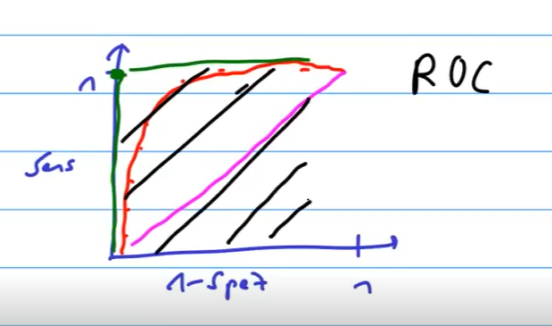
ROC Curve
?
Poisson Verteilung / Poisson Regression
Wie sieht die Poisson Verteilung aus?
?
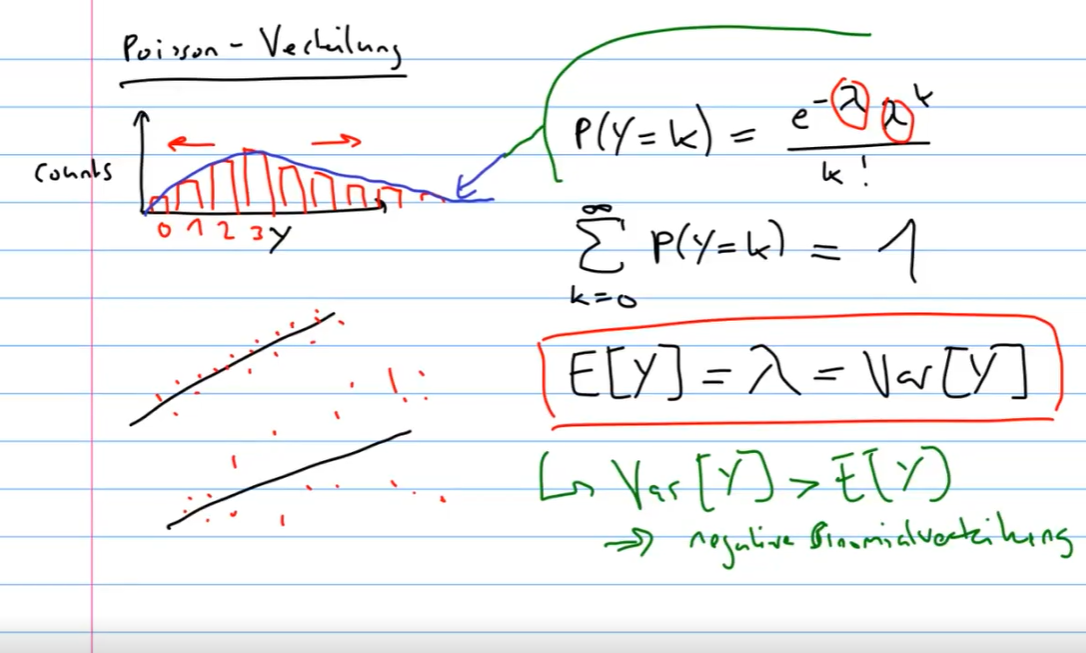
Poisson Regression
Was ist die Poisson Regression?
?
Poisson Regression wird verwendet, um die Anzahl der Ereignisse in einem festen Intervall zu modellieren. Es ist geeignet für Zähldaten, die die Poisson-Verteilung befolgen.
Die Modellgleichung lautet:
wobei:
die erwartete Anzahl der Ereignisse ist. die Prädiktoren sind. die Regressionskoeffizienten sind.
Die linke Seite der Gleichung ist der Logarithmus der Rate, und die rechte Seite ist eine lineare Funktion der Prädiktoren.
Was macht die Poissonverteilung für eine Starke Annahme? :: Varianz = Erwartungswert
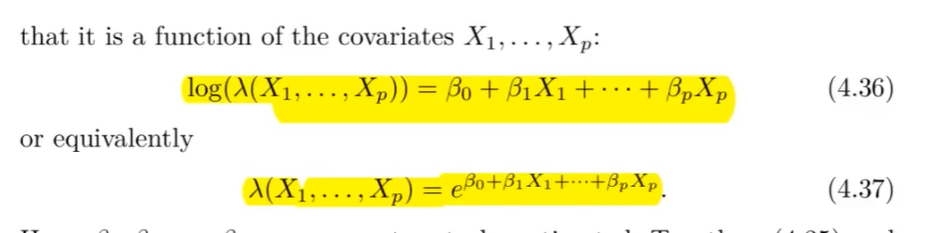
Durch das Umschreiben von den Theremen, kann man schön die rechte Seite immer eine Linreg machen
?
All diese Regressionen hängen zusammen, ungefähr die gleiche Struktur in einer Theorie. Meistens reicht eine Funktion ein eine GLM funktion. --> Linkfunction
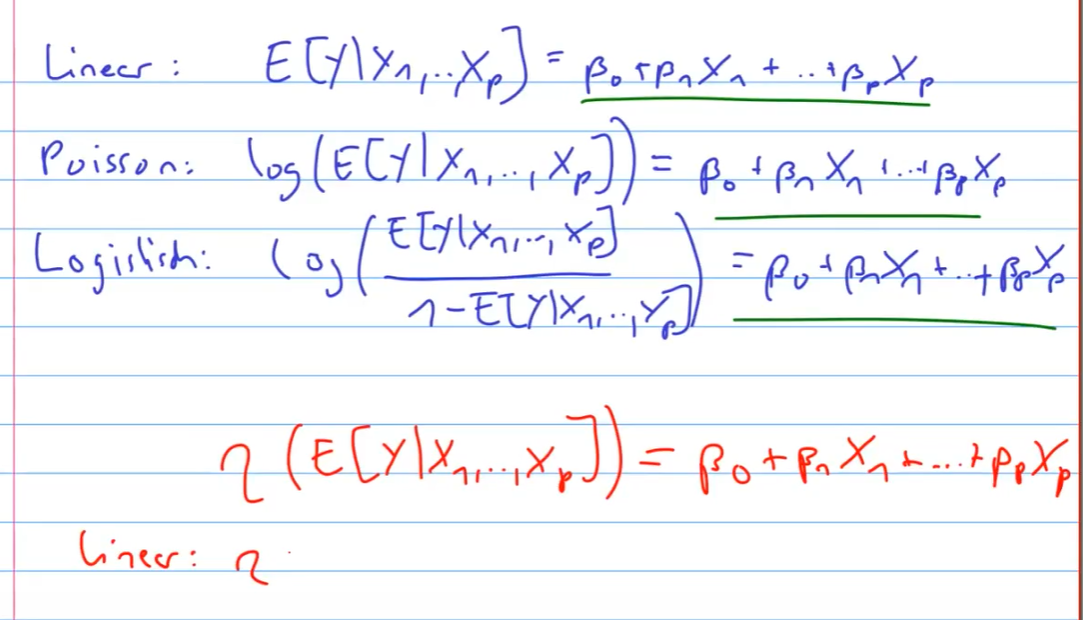

Generalized Linear Models (GLMs)
Was sind die GLM?
?
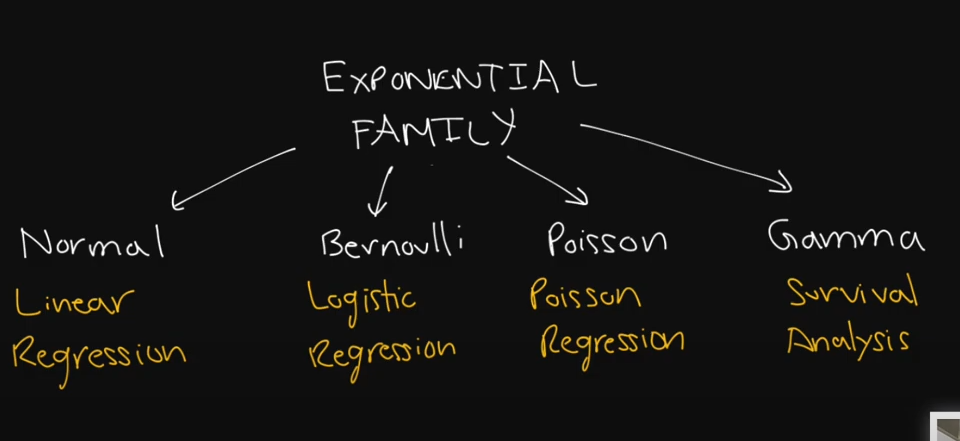
Übersicht: In diesem Kurs wurden drei GLMs behandelt: Gaussian, Binomial und Poisson.
Link-Funktion: Transformation des Mittelwerts durch eine lineare Funktion:
- Linear:
- Logistisch:
- Poisson:
Varianzfunktionen: Jede GLM hat charakteristische Varianzfunktionen.
Modellanpassung: Die Modelle werden mittels Maximum-Likelihood angepasst. Zusammenfassungen werden in R mit der Funktion glm() erzeugt.
Weitere GLMs: Gamma, Negative-binomial, Inverse Gaussian und mehr.
Resampling Methods
Was ist eine Cross Validation?
?
Cross-Validation ist eine Methode zur Schätzung des Testfehlers eines Modells, indem das verfügbare Trainingsdaten in mehrere Teilmengen aufgeteilt wird.
Validation Set Approach
Was ist der Validation Set Approche?
?
- Das Trainingsdatensatz wird zufällig in Trainings- und Testmengen aufgeteilt.
- Modell wird auf das Trainingsset angepasst und auf das Testset angewendet.
- Der Fehler im Testset dient als Schätzung für den Testfehler.
Nachteile:
- Hohe Variabilität, abhängig von der zufälligen Aufteilung.
- Das Modell wird auf weniger Daten trainiert, was den Fehler überschätzen kann.
Leave-One-Out Cross-Validation (LOOCV)
Was ist LOOCV oder auch Leave one Out Cross Validation?
?
- Jede Beobachtung wird einmal als Testset verwendet, während der Rest als Trainingsset dient.
- Modell wird ( n ) Mal angepasst und der Durchschnittsfehler wird berechnet.
Vorteile:
- Weniger variabel, da alle Datenpunkte verwendet werden.
- Weniger Bias, da fast das gesamte Datenset verwendet wird.
Nachteil:
- Kann rechnerisch aufwendig sein.
K-Fold Cross-Validation
Was ist KFold Cross Validation?
?
- Daten werden in ( K ) gleichgroße Gruppen aufgeteilt.
- Jede Gruppe wird einmal als Testset und der Rest als Trainingsset verwendet.
- Durchschnittsfehler wird berechnet.
Vorteile:
- Weniger rechnerisch aufwendig als LOOCV.
- Besseres Bias-Varianz-Verhältnis.
Typischerweise wird ( K = 5 ) oder ( K = 10 ) gewählt.
Was ist Bootstrapping?
?
Der Bootstrap ist eine Methode zur Schätzung der Unsicherheit eines Modells oder Parameters durch wiederholtes Ziehen von Stichproben mit Zurücklegen aus dem Originaldatensatz.
- Beispiel: Schätzung des Risikos einer Investition durch Bootstrapping von Renditen.
- Ein Datensatz wird mehrfach mit Zurücklegen gezogen, um viele Bootstrapped-Datensätze zu erzeugen.
- Diese werden verwendet, um Schätzungen und deren Variabilität zu berechnen.
Cross_validation:
Bootrap --> Used in Random Forest see Bagging:

Linear Model Selection & Regularization
Hier sind die wichtigsten Konzepte und Formeln von der angegebenen Webseite im Stil der bisherigen Erklärungen:
Best Subset Selection
Was ist Subset Selection?
?
Best Subset Selection passt separate Modelle für jede mögliche Kombination der Prädiktoren an:
Das beste Modell wird basierend auf Kriterien wie (R^2) oder Kreuzvalidierungsfehler ausgewählt.
Stepwise Selection
Was ist Stepwise Selection?
?
Stepwise Selection ist eine Methode zur Auswahl der besten Prädiktoren für ein Modell, indem Variablen iterativ hinzugefügt oder entfernt werden. Es gibt drei Hauptarten: dabei wird das p-value verwendet welcher der hoecchste hat entfernt oder tiefsteter hinzugefuegt.
Forward Selection:
- Beginnt mit keinem Prädiktor und fügt schrittweise den Prädiktor hinzu, der die Modellanpassung am meisten verbessert.
Backward Selection:
- Beginnt mit allen Prädiktoren und entfernt schrittweise den Prädiktor, der die Modellanpassung am wenigsten verschlechtert.
Stepwise Selection:
- Kombiniert Forward und Backward Selection, indem es Prädiktoren hinzufügt und entfernt, um das beste Modell zu finden.
Optimal Model Selection
Was ist die Optimale Model Section?
?
Die Auswahl des besten Modells erfolgt durch Schätzung des Testfehlers mittels Kreuzvalidierung oder Anpassung des Trainingsfehlers (z.B. (C_p), (AIC), (BIC), adjusted-(R^2)).
Shrinkage Methods
Was macht eine Shrinkage Method?
?
Shrinkage-Methoden passen ein Modell mit allen Prädiktoren an und schrumpfen die Koeffizienten in Richtung Null.
Ridge Regression
Wie sieht die Ridge Regression aus?
?
Minimiert die Funktion:
Dies reduziert die Varianz auf Kosten eines kleinen Bias.
Lasso Regression
Wie sieht die Lasso Regression aus?
?
Minimiert die Funktion:
Lasso schrumpft einige Koeffizienten auf genau Null, was eine Variablenselektion ermöglicht.
Dimension Reduction Methods
Was ist eine Dimensions Reduction?
?
Reduzieren die Dimensionen des Datensatzes durch Projektion auf ein (M)-dimensionales Teilraum.
Principal Components Analysis (PCA)
Fuer was verwendet man PCA?
?
Identifiziert die Hauptrichtungen der Variabilität in den Daten und projiziert die Prädiktoren auf diese Komponenten.
Partial Least Squares (PLS)
Was ist Partial Least Squares?
?
Partial Least Squares (PLS) ist eine Technik zur Dimensionenreduktion, die sowohl die Prädiktoren als auch die Antwortvariablen berücksichtigt. PLS projiziert die Prädiktoren auf neue latente Variablen (Komponenten), die maximale Kovarianz mit der Antwortvariablen haben.
Algorithmus:
- Berechnung der Gewichtungsvektoren, die die Prädiktoren und die Antwortvariablen maximieren.
- Projektion der Prädiktoren und der Antwortvariablen auf diese Gewichtungsvektoren.
- Anpassen eines linearen Modells an die projizierten Daten.
PLS ist besonders nützlich, wenn die Anzahl der Prädiktoren groß ist und Multikollinearität vorliegt. Weitere Details finden Sie auf ISLR Chapter 6 - Linear Model Selection & Regularization.
Considerations in High Dimensions
Was sollte man in hohen Dimensionen beachten?
?
Bei vielen Prädiktoren sollte man Methoden wie Subset Selection, Ridge Regression, Lasso oder PCA verwenden. Traditionelle Maßzahlen wie (R^2) sind ungeeignet; stattdessen sollte man Kreuzvalidierungsfehler berichten.
Weitere Details und ausführliche Erklärungen finden Sie auf der Webseite ISLR Chapter 6 - Linear Model Selection & Regularization.
AIC (Akaike Information Criterion)
AIC Akaike Information Criterion
?
AIC ist ein Maß zur Modellbewertung, das sowohl die Anpassungsgüte als auch die Komplexität des Modells berücksichtigt:
- ( k ): Anzahl der geschätzten Parameter
- ( L ): Maximierter Wert der Likelihood-Funktion des Modells
BIC (Bayesian Information Criterion)
BIC Bayesian Information Criterion
?
BIC ist ähnlich wie AIC, bestraft jedoch komplexere Modelle stärker:
- ( n ): Anzahl der Datenpunkte
Mean Squared Error (MSE)
MEAN Square Error
?
MSE misst den durchschnittlichen quadratischen Fehler zwischen den beobachteten und vorhergesagten Werten:
- ( y_i ): Beobachteter Wert
- ( \hat{y}_i ): Vorhergesagter Wert
Adjusted ( R^2 )
Adjusted R2?
?
Adjusted ( R^2 ) ist eine Anpassung des ( R^2 )-Werts, die die Anzahl der Prädiktoren im Modell berücksichtigt:
- ( R^2 ): Bestimmtheitsmaß
- ( n ): Anzahl der Beobachtungen
- ( k ): Anzahl der Prädiktoren
Die Probleme von Regularisierung / Shrinkage
?
- Problem 1:
- Problem 2: Overfitting
- Problem 3: Feature Selection
Regularisierung
?
Moving Boyond Linearity
Hier sind die wichtigsten Konzepte und Formeln von der angegebenen Webseite im Stil der bisherigen Erklärungen:
Polynomial Regression
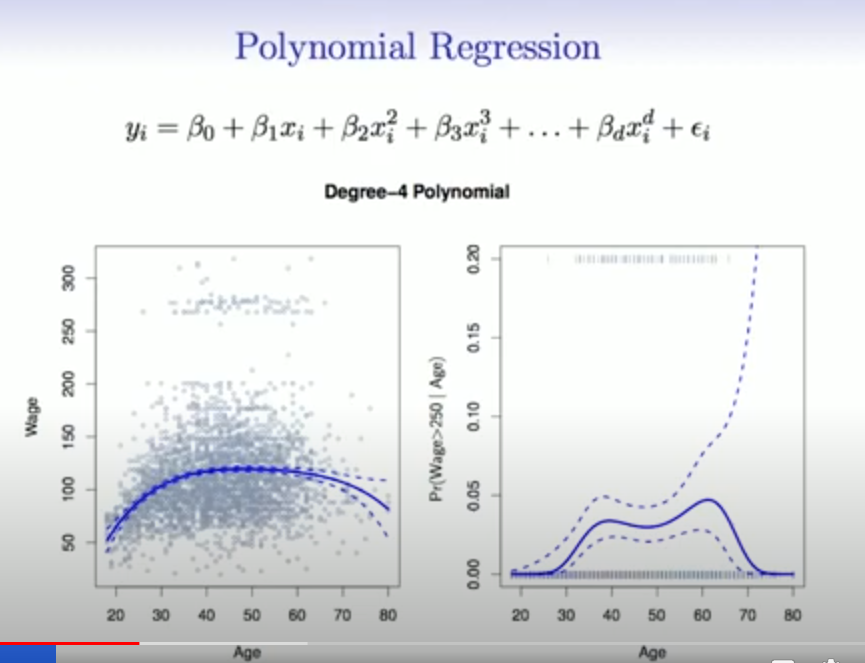
Wie sieht die Polynominale Regresion aus?
?
Polynomial regression erweitert die lineare Regression durch Hinzufügen zusätzlicher Prädiktoren, die Potenzen der ursprünglichen Prädiktoren sind:
Dies ermöglicht das Modellieren nichtlinearer Beziehungen zwischen Prädiktoren und Antwortvariablen.
Step Functions
Was ist eine Step Function?
?
Step Functions unterteilen den Bereich von (X) in Intervalle und passen innerhalb jedes Intervalls eine Konstante an:
Dies ermöglicht unterschiedliche konstante Werte für verschiedene Bereiche von (X).
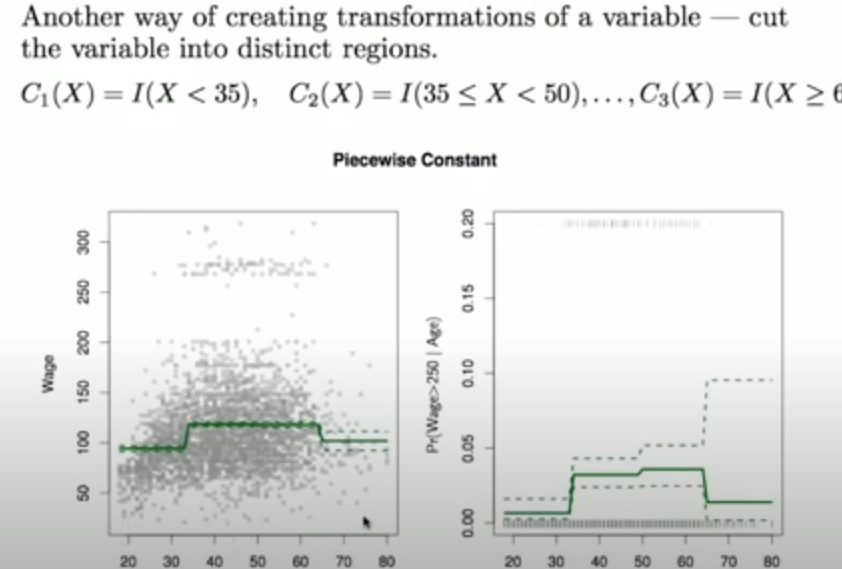
I ist eine Idicator funktion die binary zurueck gibt.
Was sind gute Eigenschaften von Stepfunctions?
?

Basis Functions
Wie sind Basis Function definiert?
?
Basis Functions wenden eine Familie von Funktionen auf einen Prädiktor an:
Beispiele sind Polynomiale und Stückweise Konstante.
Piecewise Polynomial Regression
Was ist die Piecewise Polynominal Regression?
?
Piecewise Polynomial Regression unterteilt den Prädiktorraum in Intervalle und passt in jedem Intervall ein separates Polynom an. Dadurch können komplexe, nichtlineare Beziehungen modelliert werden.
Stückweise Lineare Regression:
Stückweise Polynomiale höheren Grades:
- ( \beta_{j,i} ): Koeffizienten der Polynomiale im (i)-ten Intervall
- ( d ): Grad des Polynoms
- ( a, b, c, z, w ): Grenzwerte der Intervalle
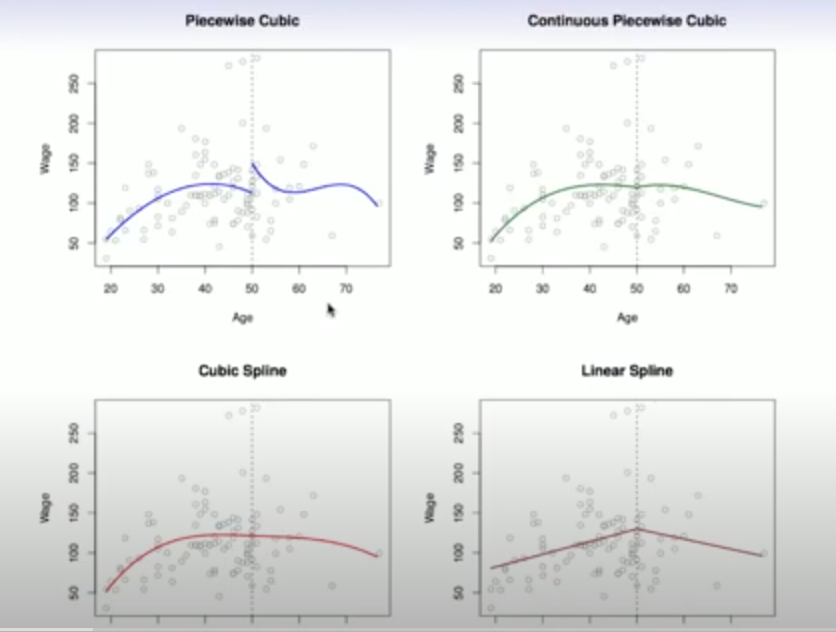
Piecewise Polynomial Regression bietet Flexibilität und Genauigkeit, indem sie die Modellkomplexität auf die Daten anpasst.
Lineare Splines
Was sind Lineare Splines?
Ein linearer Spline mit Knoten bei
Wir können dieses Modell darstellen als:
wobei die (b_k) Basisfunktionen sind:
Hier bedeutet (()_+) den positiven Teil, d.h.
: Beobachteter Wert für die -te Beobachtung : Regressionskoeffizienten : Basisfunktionen : Prädiktorwert für die -te Beobachtung : Knotenpunkte : Fehlerterm
Kubische Splines
Was sind cubicsplines?
?
Ein kubischer Spline mit Knoten bei
Wir können dieses Modell mit abgeschnittenen Potenz-Basisfunktionen darstellen:
wobei:
Hier bedeutet
: Beobachteter Wert für die -te Beobachtung : Regressionskoeffizienten : Basisfunktionen : Prädiktorwert für die -te Beobachtung : Knotenpunkte : Fehlerterm
Natürliche kubische Splines
Was ist ein natuerlicher kubischer spline?
?
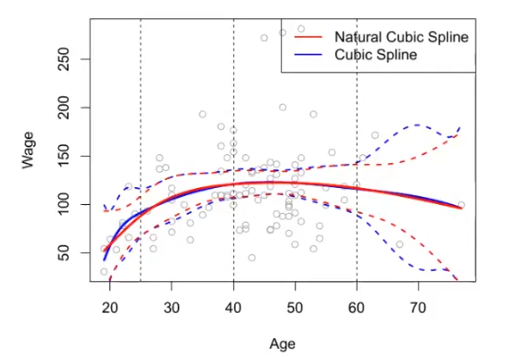
Ein natürlicher kubischer Spline extrapoliert linear über die Randknoten hinaus. Dies fügt 4 (2 × 2) zusätzliche Einschränkungen hinzu und ermöglicht es uns, mehr interne Knoten für die gleichen Freiheitsgrade wie ein regulärer kubischer Spline zu setzen.
- Randknoten: Stellen sicher, dass der Spline an den Rändern linear wird.
- Freiheitsgrade: Anzahl der Parameter, die zur Anpassung des Splines verwendet werden.
Die Grafik zeigt den Unterschied zwischen einem natürlichen kubischen Spline (rote Linie) und einem regulären kubischen Spline (blaue Linie).
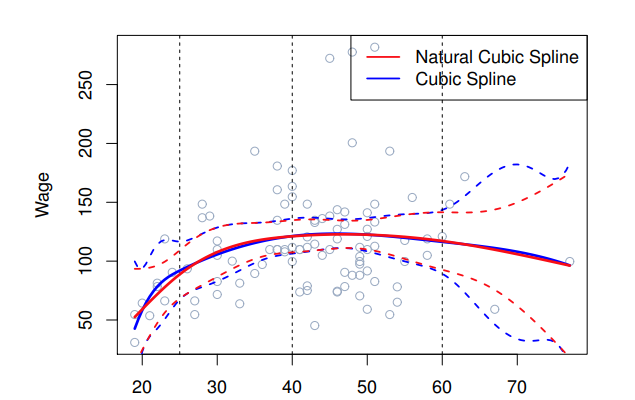
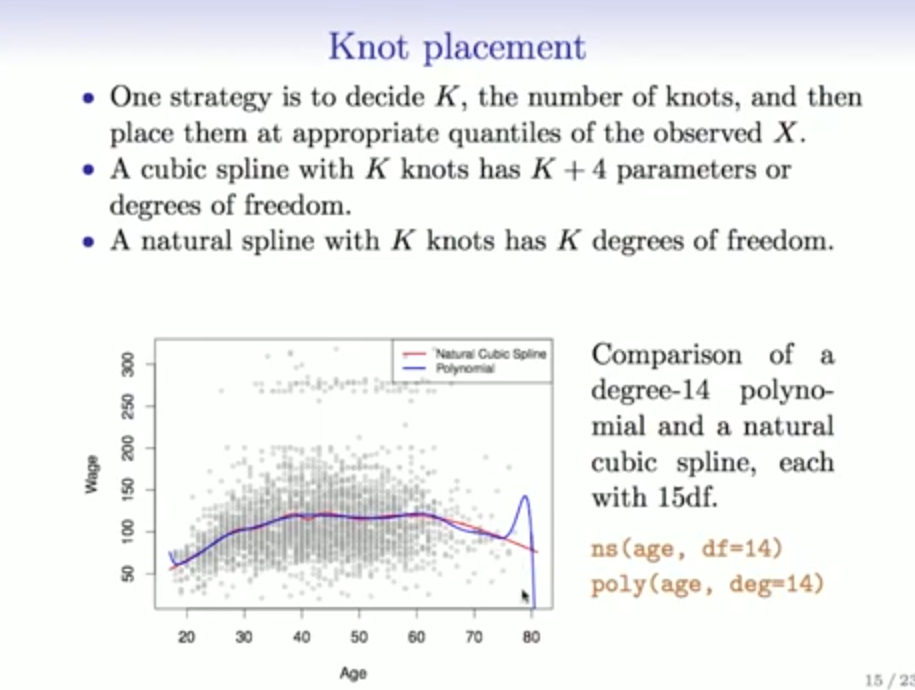
Warum sind Polynomial Regressions schlechter als Splines?
?
Regression Splines
Was sind Regression splines und wie Berechnet man sie?
?
Regression Splines erweitern die Polynom- und Stückweise-Konstante-Regression:
Splines sind glatt und kontinuierlich an den Knotenpunkten.
Smoothing Splines
Was sind Smoothing Splines und wie berechnet man sie?
?
Das gute an Smoothing Splines ist, dass man splines fitten kann ohne, dass man die Knots placen muss.
Smoothing Splines minimieren die Summe der quadrierten Fehler und eine Glattheitsstrafe:
Dies führt zu glatten Funktionen, die gut zu den Daten passen.
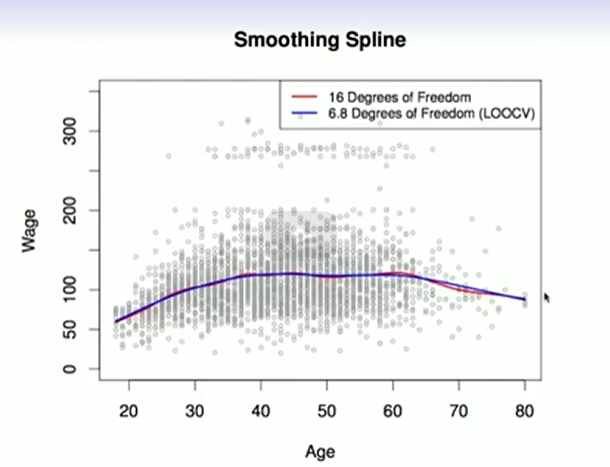
Local Regression
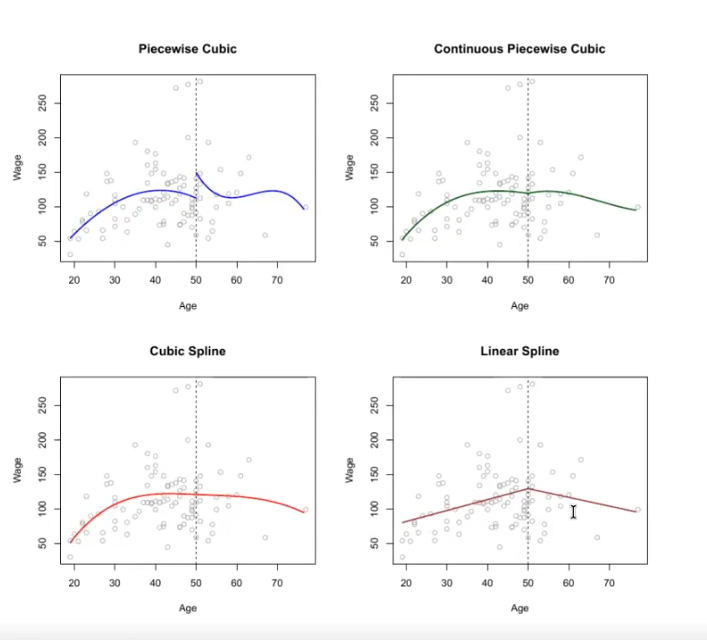
Was ist Local Regression und wie sieht die Formel aus?
?
Local Regression passt lokale lineare Modelle an Punkte nahe einem Zielpunkt an:
Dies ermöglicht flexible, nichtlineare Anpassungen.
Generalized Additive Models (GAMs)
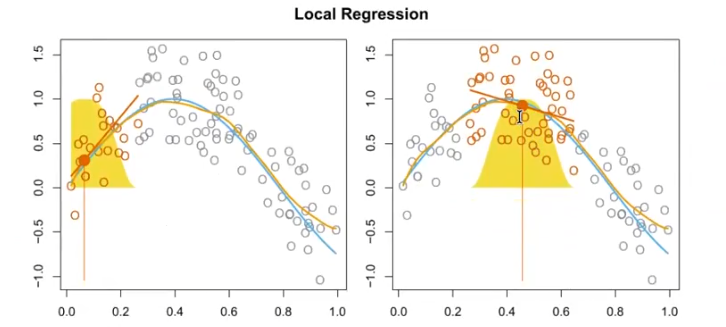
was sind General additive model?
?
GAMs ermöglichen nichtlineare Funktionen jedes Prädiktors, während sie Additivität beibehalten:
GAMs kombinieren Flexibilität und Interpretierbarkeit.
Generalized Additive Models (GAMs)
Wie kann die formel von Gams ohne summe daargestellt werden?
?
GAMs erlauben flexible Nichtlinearitäten in mehreren Variablen, behalten aber die additive Struktur linearer Modelle bei.
: Beobachteter Wert für die -te Beobachtung : Interzept : Glättungsfunktionen der Prädiktoren : Prädiktorwert für die -te Beobachtung und den -ten Prädiktor : Fehlerterm
Die Diagramme zeigen, wie die Funktionen
Generalized Additive Models (GAMs)
Koennen in Gams auch wechselwirkungen einbezogen werden?
?
GAMs sind additiv, obwohl Wechselwirkungen niedriger Ordnung auf natürliche Weise durch bivariate Glätter oder Wechselwirkungen der Form
- Additive Modelle: Jede Komponente wird separat angepasst und addiert.
- Bivariate Glätter: Glättungsmethoden für zwei Variablen gleichzeitig.
- Wechselwirkungen: Interaktionen zwischen Variablen, die im Modell berücksichtigt werden.
GAMs bieten Flexibilität bei der Modellierung nichtlinearer Beziehungen und Wechselwirkungen in den Daten.
GAMs für Klassifikation
Wie verwendet man Gams fuer Klassification?
?
Generalized Additive Models (GAMs) können auch für Klassifikationsprobleme verwendet werden. Die logistische Regression wird als additive Modelle erweitert:
: Wahrscheinlichkeit des Ereignisses : Interzept : Glättungsfunktionen der Prädiktoren
In R kann dies mit der gam() Funktion durchgeführt werden, wie im Beispiel:
: Jahr : Alter : Bildung
Polynominal Regression (Linear Regression)
?
- Hat viel mehr gefahren wie Nutzen
Polynominal Regression (Logitic Regression)
?
Was sind Step Functions
?
Step Function
?
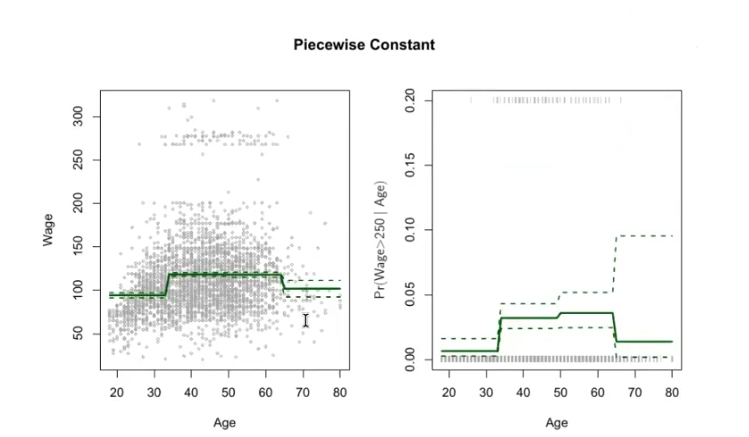
Step Function als Generalisiertes Modell Beispiel Logitische Regression
?
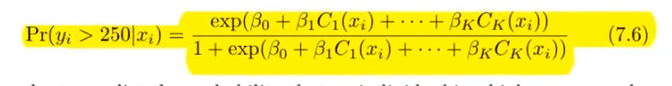
Regression splines
?
Local regression
?
Generalized additive models
?
Generalized Additive Models (GAMs)
Was sind GAMS?
?
Generalized Additive Models (GAMs) ermöglichen es, die Beziehung zwischen der Antwortvariablen und mehreren Prädiktoren durch additive nichtlineare Funktionen darzustellen.
Das Modell wird wie folgt formuliert:
ist die Antwortvariable. ist der Interzept. sind nichtlineare Glättungsfunktionen der Prädiktoren . ist der Fehlerterm.
GAMs kombinieren Flexibilität und Interpretierbarkeit, da jede nichtlineare Funktion einzeln geschätzt und interpretiert werden kann.
was bringt ein spline was ein piecewise polynom nicht hat?
?
kontinuitaet sprich die linie hat keine sprungstelle, sommit kann stetigkeit die derivative berechnet werden.
basis function
?
todo
Kontinuitaet
?

allgemein: K+d+1 freie Parameter
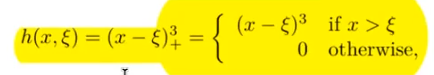
Was sind natruerliche Splines ?
?
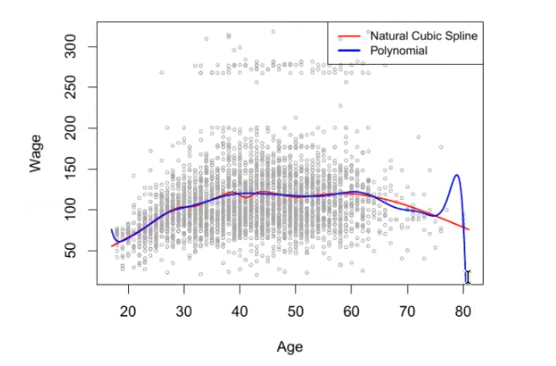
Nachteil Polynominal Regression
?
Kolmogorov-arnod Networks
?
todo
Treebased Models
Hier sind die wichtigsten Konzepte und Formeln von der angegebenen Webseite im Stil der bisherigen Erklärungen:
Basics of Decision Trees
Decision Trees segmentieren den Prädiktorraum in einfache Regionen. Jede Beobachtung wird einer Region zugeordnet, und die Vorhersage erfolgt durch den Mittelwert oder Modus der Trainingsbeobachtungen in dieser Region.
Regression Trees:
Pruning:
Classification Trees
Klassifikationsbäume sagen qualitative Antworten voraus. Die Vorhersage erfolgt durch die am häufigsten vorkommende Klasse im Endknoten.
Gini Index:
Cross-Entropy:
Bagging
Bagging reduziert die Varianz durch das Erstellen vieler Bootstrapped-Trainingsdatensätze, das Bauen mehrerer Bäume und das Mittelwerten der Vorhersagen.
Out-of-Bag (OOB) Error:
OOB-Beobachtungen werden verwendet, um den Testfehler des Modells zu schätzen.
Random Forests
Random Forests verbessern Bagging durch Dekorrelieren der Bäume. Bei jeder Aufteilung wird eine zufällige Stichprobe von (m) Prädiktoren als Aufteilungskandidaten gewählt.
Wichtigkeit der Prädiktoren:
Wichtige Prädiktoren werden durch die Verringerung des Gini-Index oder der RSS bei Aufteilungen bestimmt.
Boosting
Boosting baut viele Bäume sequentiell auf, wobei jeder Baum Informationen aus dem vorhergehenden Baum verwendet.
Boosting Algorithmus:
Weitere Details und ausführliche Erklärungen finden Sie auf der Webseite ISLR Chapter 8 - Tree-Based Methods.
Support Vektor Machines
Hier sind die wichtigsten Konzepte und Formeln von der angegebenen Webseite im Stil der bisherigen Erklärungen:
Maximal Margin Classifier
Der Maximal Margin Classifier trennt Klassen durch einen Hyperplane mit maximalem Abstand zu den nächsten Datenpunkten beider Klassen.
Betreffend:
Support Vector Classifier
Der Support Vector Classifier erlaubt einige Fehler und verbessert Robustheit.
Betreffend:
Support Vector Machines
Support Vector Machines erweitern Support Vector Classifier durch Kernel, die nichtlineare Entscheidungsgrenzen ermöglichen.
Kernels:
Polynom-Kernel:
Radial Kernel:
SVMs with More than Two Classes
One-Versus-One:
Entwickelt mehrere SVMs, die jeweils zwei Klassen vergleichen.
One-Versus-All:
Entwickelt mehrere SVMs, die jede Klasse gegen alle anderen vergleichen.
Die Testbeobachtung wird der Klasse zugeordnet, für die der Ausdruck:
am größten ist.
SVMs vs Logistic Regression
SVMs und Logistische Regression haben ähnliche Verlustfunktionen und geben oft ähnliche Ergebnisse. Bei gut getrennten Klassen performen SVMs besser, während Logistische Regression bei mehr Überlappung besser abschneidet.
Weitere Details und ausführliche Erklärungen finden Sie auf der Webseite ISLR Chapter 9 - Support Vector Machines.
Unsuppervised Learning
Hier sind die wichtigsten Konzepte und Formeln von der angegebenen Webseite im Stil der bisherigen Erklärungen:
Principal Components Analysis (PCA)
PCA reduziert die Dimensionen eines Datensatzes, indem es neue, unkorrelierte Variablen, die Principal Components, berechnet.
Erster Principal Component:
Die
K-Means Clustering
K-Means Clustering teilt den Datensatz in (K) Cluster auf, sodass die Summe der quadratischen Abweichungen innerhalb der Cluster minimiert wird.
Algorithmus:
- Zufällige Zuweisung von Beobachtungen zu Clustern.
- Berechnung der Cluster-Zentroiden.
- Neuzuordnung der Beobachtungen basierend auf der Nähe zu den Zentroiden.
- Wiederholung bis zur Konvergenz.
Hierarchical Clustering
Hierarchical Clustering erzeugt eine hierarchische Darstellung der Daten in Form eines Dendrogramms.
Algorithmus:
- Berechnung der Distanzen zwischen allen Beobachtungen.
- Fusion der ähnlichsten Cluster.
- Wiederholung bis alle Beobachtungen in einem Cluster sind.
Linkage-Methoden:
- Complete Linkage: Maximale Distanz zwischen den Beobachtungen in zwei Clustern.
- Single Linkage: Minimale Distanz.
- Average Linkage: Durchschnittliche Distanz.
- Centroid Linkage: Distanz zwischen den Zentroiden der Cluster.
Practical Issues in Clustering
Entscheidungen wie die Standardisierung von Variablen und die Wahl der Distanz- und Linkage-Methode beeinflussen die Ergebnisse.
Validierung ist schwierig, und die Ergebnisse sollten als Ausgangspunkt für Hypothesen und weitere Untersuchungen betrachtet werden.
Weitere Details und ausführliche Erklärungen finden Sie auf der Webseite ISLR Chapter 10 - Unsupervised Learning.
Week 13 (S. 301-307)
Smoothing Splines
?

Loss function von Smoothing Splines
?
todo
Freiheitsgrade von Smoothing Splines
?
todo
Unterschied von Regression Splines und Smoothing Splines
?
todo
Was ist das Setting der Linearen Regression?
?
 ]]
]]
Freiheitsgrade Splines
?

Week 14 (S. 307-311)
Question Answering
LE 1: Theoretische Grundlagen des STL
1. Was wird im Statistical Learning untersucht?
Statistical Learning untersucht Methoden zur Analyse und Interpretation komplexer Daten. Es umfasst Werkzeuge zur Modellierung der Beziehung zwischen Variablen, sowohl in überwachten (Vorhersage von Outputs basierend auf Inputs) als auch in unüberwachten (Strukturierung und Mustererkennung in Daten ohne explizite Outputs) Kontexten.
2. Fasse deine Erkenntnisse aus diesem Kompetenzmodul auf einer A4-Seite zusammen.
Das Kompetenzmodul vermittelt die Grundlagen des Statistical Learning, einschließlich der Definitionen von überwachten und unüberwachten Lernmethoden, des Bias-Variance-Tradeoffs, und der Unterscheidung zwischen parametrischen und nicht-parametrischen Modellen. Es behandelt wichtige Konzepte wie den reduzierbaren und nicht-reduzierbaren Fehleranteil und stellt verschiedene Modellierungsansätze vor, darunter lineare und nicht-lineare Modelle, sowie Methoden zur Modellbewertung und -auswahl.
3. Was steckt im Fehler
Der Fehler
4. Charakterisiere den reduzierbaren und den nicht-reduzierbaren Anteil von
- Reduzierbarer Anteil: Der Teil des Fehlers, der durch ein besseres Modell reduziert werden kann. Dieser umfasst den Bias und die Varianz des Modells.
- Nicht-reduzierbarer Anteil: Der Fehler, der nicht durch ein Modell reduziert werden kann, da er aus zufälligen Störgrößen und unvorhersehbaren Einflüssen besteht.
5. Was ist der Unterschied zwischen einem parametrischen und einem nicht-parametrischen Modell? Gib Beispiele.
- Parametrisches Modell: Diese Modelle nehmen eine spezifische Form für die Funktion
an (z.B. lineare Regression). Sie sind effizient und einfach zu interpretieren, haben aber einen hohen Bias, wenn die Modellannahme falsch ist. - Nicht-parametrisches Modell: Diese Modelle nehmen keine spezifische Form für
an (z.B. KNN, Entscheidungsbäume). Sie sind flexibel und haben einen niedrigen Bias, aber sie können viele Daten benötigen und anfällig für Overfitting sein.
6. Liste die in diesem Kompetenzmodul untersuchten Modelle auf. In welche Untergruppen können sie aufgeteilt werden?
Untersuchte Modelle:
- Lineare Regression
- KNN
- Entscheidungsbäume
- SVM
- Clustering
Untergruppen:
- Überwachtes Lernen: Regression (lineare Regression), Klassifikation (KNN, SVM)
- Unüberwachtes Lernen: Clustering
7. Welche der eingeführten Modelle können mit qualitativen Prädiktoren umgehen?
Modelle wie die logistische Regression und Entscheidungsbäume können mit qualitativen Prädiktoren umgehen, indem sie diese in Dummy-Variablen umwandeln oder Kategorien direkt in die Analyse einbeziehen.
8. Welche Masse existieren, um die Qualität eines Fits zu bestimmen? Was sind ihre Vor- und Nachteile?
- Klassifikation:
- Accuracy: Einfach zu interpretieren, aber nicht geeignet bei unausgeglichenen Datensätzen.
- F1-Score: Berücksichtigt sowohl Präzision als auch Recall, besser bei unausgeglichenen Datensätzen.
- Regression:
- MSE (Mean Squared Error): Einfach zu interpretieren, empfindlich gegenüber Ausreißern.
- R^2: Gibt den Anteil der Varianz an, der durch das Modell erklärt wird, kann jedoch bei komplexen Modellen irreführend sein.
9. Erkläre den Bias-Variance Trade-Off an einem Training und Validierungsset.
Ein Modell mit hoher Kapazität (Komplexität) hat niedrigen Bias, aber hohe Varianz, was zu Overfitting führen kann. Ein einfaches Modell hat hohen Bias, aber niedrige Varianz, was zu Underfitting führt. Die richtige Modellkapazität minimiert den Gesamtfehler und berücksichtigt sowohl Bias als auch Varianz.
10. Was ist der Bayes Classifier? Warum ist KNN eine Annäherung des Bayes Classifiers?
Der Bayes Classifier weist jeder Beobachtung die Klasse mit der höchsten posterioren Wahrscheinlichkeit zu. KNN approximiert dies, indem es die Mehrheit der Klassen in den K nächsten Nachbarn verwendet.
11. Erkläre den Bias-Variance-Tradeoff am Beispiel von KNN oder eines Regression Splines.
- KNN: Bei kleinem
hat das Modell niedrigen Bias, aber hohe Varianz. Bei großem steigt der Bias, die Varianz sinkt. - Regression Splines: Mit vielen Knotenpunkten (Flexibilität) hat das Modell niedrigen Bias, aber hohe Varianz. Wenige Knotenpunkte führen zu hohem Bias, aber niedriger Varianz.
12. Erkläre, wie die Natur der Daten die Kurven im Bias-Variance-Tradeoff beeinflusst.
Wenn Daten komplex und variabel sind, benötigen Modelle mit höherer Kapazität, um Muster zu erfassen, was die Varianz erhöht. Einfache Daten können durch Modelle mit niedriger Kapazität gut beschrieben werden, was den Bias reduziert.
13. Was ist das ‘No free lunch’-Theorem des Statistical Learning?
Das 'No free lunch'-Theorem besagt, dass kein Modell in allen Situationen überlegen ist. Die Modellleistung hängt von der Datenstruktur und dem spezifischen Anwendungsfall ab.
14. Welche Modelle kennst du, die keine Regressionsmodelle sind?
- Klassifikationsmodelle: KNN, logistische Regression, SVM.
- Clustering-Methoden: K-Means, Hierarchical Clustering.
15. Was ist ein memory-basiertes Modell? Nenne Beispiele.
Memory-basierte Modelle speichern Trainingsdaten und verwenden sie zur Vorhersage neuer Daten. Beispiele sind KNN und Kernel-SVMs.
16. Was ist der Accuracy vs. Interpretability-Tradeoff? Warum ist Interpretierbarkeit wichtig, bzw. oft wichtiger als eine hohe Vorhersagegenauigkeit?
Ein hochgenaues Modell kann komplex und schwer interpretierbar sein, während ein einfaches Modell leichter zu verstehen ist. Interpretierbarkeit ist wichtig, um Modelle in praktischen Anwendungen zu erklären und Vertrauen zu schaffen.
LE 2: Lineare Regression
1. Was sind Residuen und welcher Verteilungsannahme müssen sie im Setting der linearen Regression folgen?
Residuen sind die Differenzen zwischen den beobachteten Werten und den durch das Modell vorhergesagten Werten. Im Setting der linearen Regression wird angenommen, dass die Residuen normalverteilt sind mit einem Mittelwert von null und konstanter Varianz (Homoskedastizität).
2. Warum sind der Residual Standard Error (RSE) und der Root-Mean-Squared Error (RMSE) im asymptotischen Limit der Anzahl Beobachtungen gleich groß?
Im asymptotischen Limit, wenn die Anzahl der Beobachtungen groß ist, konvergiert der RSE gegen den RMSE, da beide Maßzahlen im Wesentlichen die durchschnittliche Größe der Residuen messen. Der Unterschied besteht in der Freiheitsgrade-Korrektur beim RSE, die bei großer Stichprobe vernachlässigbar wird.
3. Was ist der Wertebereich der ( R^2 )-Statistik? Was ist passiert, wenn die ( R^2 )-Statistik negativ ist?
Der Wertebereich der ( R^2 )-Statistik liegt zwischen 0 und 1. Eine negative ( R^2 )-Statistik deutet darauf hin, dass das Modell schlechter abschneidet als ein einfaches Mittelwertsmodell, was bei schlecht angepassten Modellen auftreten kann.
4. Was sind die Vor- und Nachteile von linearer Regression gegenüber KNN?
- Interpretierbarkeit: Lineare Regression ist einfacher zu interpretieren als KNN.
- Kapazität: Lineare Regression hat eine geringe Kapazität und neigt zu Underfitting, während KNN eine hohe Kapazität hat und zu Overfitting neigen kann.
- Effizienz: Lineare Regression ist rechnerisch effizienter als KNN, insbesondere bei großen Datensätzen.
- Datenmenge: KNN benötigt mehr Daten, um genaue Vorhersagen zu treffen, während die lineare Regression auch mit weniger Daten gut funktioniert.
5. Für die lineare Regression lassen sich Standardabweichungen auf die geschätzten Koeffizienten bestimmen. Wie könntest du diese Standardabweichungen auch ohne Formel schätzen?
Die Standardabweichungen der geschätzten Koeffizienten können durch Bootstrap-Methoden geschätzt werden, bei denen wiederholt Stichproben mit Zurücklegen aus dem Datensatz gezogen und die Modellparameter neu geschätzt werden.
6. Was ist der t-Test und welche Rolle spielt er in der linearen Regression? Wo führt er zu Problemen?
Der t-Test wird verwendet, um zu testen, ob ein Regressionskoeffizient signifikant von null verschieden ist. Er prüft die Nullhypothese, dass der Koeffizient keinen Einfluss hat. Probleme treten auf, wenn die Annahmen der Normalverteilung und Homoskedastizität der Residuen verletzt sind.
7. Schreibe das Setting der Multiplen Linearen Regression in Vektor- und Matrixform auf.
In Vektor- und Matrixform wird die multiple lineare Regression wie folgt dargestellt:
wobei
8. Was ist die Motivation, für das Fitten der Regressionsparameter Least Squares zu benutzen? Warum nicht zum Beispiel einen Mean Absolute Error (MAE, L1-Distanz zwischen Vorhersage und tatsächlichen Werten)?
Least Squares (Kleinste Quadrate) minimiert die Summe der quadrierten Residuen und führt zu einfacheren mathematischen Lösungen und Optimierung. Mean Absolute Error (MAE) hat den Vorteil, robust gegenüber Ausreißern zu sein, aber es führt zu komplexeren Optimierungsproblemen, da es nicht differenzierbar ist.
9. Wie ist die F-Statistik im Setting der Multiplen Linearen Regression zu interpretieren?
Die F-Statistik testet die Nullhypothese, dass alle Regressionskoeffizienten außer dem Interzept gleich null sind. Eine signifikant hohe F-Statistik deutet darauf hin, dass das Modell mit den Prädiktoren besser ist als ein Modell ohne Prädiktoren.
10. Wie können im linearen Regressionssetting qualitative Variablen berücksichtigt werden? Wie sind die Modellparameter zu interpretieren?
Qualitative Variablen können durch Dummy-Variablen kodiert werden. Modellparameter repräsentieren dann die Veränderung der abhängigen Variablen im Vergleich zur Referenzkategorie.
11. Was ist Multikollinearität? Warum ist sie in der linearen Regression ein Problem? Wie kannst du herausfinden, ob drei oder mehr Variablen eine multikollineare Beziehung haben?
Multikollinearität tritt auf, wenn zwei oder mehr Prädiktoren stark korreliert sind, was die Schätzung der Koeffizienten ungenau macht. Sie kann durch Variance Inflation Factor (VIF) und Korrelationsmatrizen untersucht werden.
12. Was ist ein additives Modell? Warum ist die einfache lineare Regression additiv? Was sind die Einschränkungen eines additiven Modells? Wie kannst du diese zum Teil umgehen? Was ist das hierarchische Prinzip zum Umgang mit Interaktionsvariablen? Was sind Haupteffekte? Warum ist polynomiale Regression immer noch ein lineares Modell?
Additive Modelle kombinieren die Effekte der Prädiktoren additiv. Lineare Regression ist additiv, da sie die Summe der Prädiktor-Effekte modelliert. Einschränkungen bestehen in der Unfähigkeit, komplexe Interaktionen zu modellieren, die durch Interaktionsterme und hierarchisches Modellieren teilweise umgangen werden können. Haupteffekte sind die Einzelwirkungen der Prädiktoren. Polynomiale Regression ist linear in den Koeffizienten, daher ein lineares Modell.
13. Was ist Heteroskedastizität? Wie steht sie zu den Modellannahmen der linearen Regression? Mit welchen Methoden kannst du wieder in ein homoskedastisches Setting zurückkommen?
Heteroskedastizität bedeutet, dass die Varianz der Residuen nicht konstant ist. Dies verletzt die Annahmen der linearen Regression. Methoden wie logarithmische Transformationen oder gewichtete Regression können helfen, Homoskedastizität zu erreichen.
14. Welche Arten von Ausreißern gibt es? Welche Art von Ausreißern beeinflusst ein lineares Regressionsmodell besonders? Mit welchem Mass kannst Ausreisser dieser Art finden?
Es gibt Ausreißer in den Prädiktoren und in den abhängigen Variablen. Leverage-Punkte (Ausreißer in den Prädiktoren) beeinflussen das Modell besonders stark. Cook’s Distance misst den Einfluss einzelner Beobachtungen auf das Modell.
15. Was ist die Maximum-Likelihood-Methode und wie kann sie im Fall der linearen und logistischen Regression benutzt werden, um das optimale Modell zu finden? Warum ist Least Squares eine Konsequenz daraus?
Die Maximum-Likelihood-Methode schätzt Parameter, die die beobachteten Daten am wahrscheinlichsten machen. In der linearen Regression führt dies zu den gleichen Ergebnissen wie Least Squares, da die Normalverteilungsannahmen der Fehler konsistent sind. In der logistischen Regression wird die Wahrscheinlichkeit der Klassenzugehörigkeit maximiert.
LE 3: Klassifikationsprobleme
1. Welche Grössen zur Beurteilung der Performance eines Klassifikationsmodells kennst du? Wie können sie auf ein Setting mit mehr als nur zwei Klassen erweitert werden? Wie beeinflusst Class Imbalance diese Grössen? Erkläre die ROC-Kurve und warum sie benutzt wird.
Performance-Messgrößen:
- Accuracy: Anteil der korrekt klassifizierten Beispiele.
- Precision: Anteil der korrekt positiv klassifizierten Beispiele.
- Recall (Sensitivity): Anteil der tatsächlich positiven Beispiele, die korrekt erkannt wurden.
- F1-Score: Harmonisches Mittel von Precision und Recall.
- ROC-Kurve (Receiver Operating Characteristic): Zeigt die True Positive Rate gegen die False Positive Rate für verschiedene Schwellenwerte. Der AUC (Area Under Curve) Wert gibt die Güte des Modells an.
Class Imbalance:
- Bei unausgeglichenen Datensätzen kann Accuracy irreführend sein. Precision, Recall und der F1-Score sind besser geeignet, um die Performance zu bewerten.
Multiclass Settings:
- Macro-Averaging: Berechnet die Metriken für jede Klasse und mittelt sie.
- Micro-Averaging: Aggregiert die Beiträge aller Klassen zur Metrik.
2. Was ist die Rolle der Sigmoid-Funktion in der logistischen Regression? Warum kann für diskrete Zielgrössen nicht einfach ein lineares Regressionsmodell verwendet werden?
Die Sigmoid-Funktion transformiert den linearen Output in einen Wert zwischen 0 und 1, der als Wahrscheinlichkeit interpretiert werden kann:
Ein lineares Regressionsmodell ist nicht geeignet für diskrete Zielgrößen, da es keine Wahrscheinlichkeiten ausgibt und die Fehlerverteilung nicht normal ist.
3. Wie sind die gefundenen Koeffizienten der logistischen Regression zu interpretieren?
Die Koeffizienten der logistischen Regression ((\beta)) geben an, wie sich die Log-Odds des Zielereignisses ändern, wenn sich der Prädiktor um eine Einheit ändert. Die Exponentialfunktion der Koeffizienten ((e^{\beta})) gibt das Odds Ratio an.
4. Was ist der Unterschied zwischen Multipler und Multinomialer Regression? Erkläre beide Settings mit Formeln. Können sie kombiniert werden?
- Multiple Regression: Nutzt mehrere Prädiktoren zur Vorhersage einer kontinuierlichen Antwort:
- Multinomiale Regression: Verwendet mehrere Prädiktoren zur Vorhersage einer kategorialen Antwort mit mehr als zwei Klassen:
Kombination: Ja, sie können kombiniert werden, um kategoriale Vorhersagen mit multiplen Prädiktoren zu treffen.
5. Was ist ein generatives Modell? Warum sind LDA, QDA und Naive Bayes generative Modelle? Was ist der Vorteil eines generativen Modells im Vergleich zu KNN oder logistischer Regression? Was sind Nachteile?
Generative Modelle modellieren die gemeinsame Verteilung der Prädiktoren und der Antwortvariable (P(X, Y)). LDA, QDA und Naive Bayes sind generative Modelle, weil sie die Verteilung (P(X|Y)) und (P(Y)) modellieren und dann Bayes' Theorem anwenden.
Vorteile:
- Besser bei kleinen Datenmengen.
- Kann fehlende Datenpunkte besser behandeln.
Nachteile:
- Annahmen über die Verteilung der Daten können ungenau sein.
- Komplexität und Rechenaufwand können hoch sein.
6. Was sind die Modellannahmen von LDA? Wie werden Klassifikationsentscheidungen getroffen? Woher kommt der Name 'Diskriminantenanalyse'? In welchem Punkt unterscheidet sich QDA zu LDA bezüglich Modellannahmen? In welchem Punkt Naive Bayes? Welches Modell ist das beste?
- Modellannahmen von LDA:
- Normalverteilte Prädiktoren in jeder Klasse.
- Gleiche Kovarianzmatrix für alle Klassen.
- Klassifikationsentscheidungen: Basieren auf der Maximierung der posterioren Wahrscheinlichkeit.
- Diskriminantenanalyse: Kommt von der Nutzung von Diskriminanzfunktionen zur Unterscheidung der Klassen.
- QDA: Erlaubt unterschiedliche Kovarianzmatrizen für jede Klasse.
- Naive Bayes: Geht von Unabhängigkeit der Prädiktoren aus.
Das beste Modell hängt vom Datensatz und den Annahmen ab. LDA ist effizient bei großen, gut getrennten Klassen, während KNN flexibel ist, aber viel Rechenaufwand erfordert.
7. LDA und Logistische Regression sind beides lineare Modelle. Warum klassifizieren sie gleiche Datensätze trotzdem mit unterschiedlichen Hyperebenen?
LDA maximiert die Trennung zwischen Klassen basierend auf den Klassenverteilungen, während logistische Regression die Wahrscheinlichkeiten für die Klassen direkt modelliert. Dies führt zu unterschiedlichen Klassifikationsgrenzen.
8. Warum ist ein Naive Bayes-Modell mit allgemeiner grundlegender Verteilung flexibler als ein QDA-Modell? Warum ist ein Naive Bayes-Modell mit Normalverteilung weniger flexibel als ein LDA-Modell?
- Naive Bayes mit allgemeiner Verteilung: Kann jede Verteilung annehmen und ist daher flexibler.
- Naive Bayes mit Normalverteilung: Macht stärkere Annahmen über die Form der Verteilung, was es weniger flexibel macht als LDA, das nur gleiche Kovarianzmatrizen voraussetzt.
9. Welches ist das beste Klassifikationsmodell? Warum kann keine einfache Aussage diesbezüglich gemacht werden? In welchem Setting ist LDA das beste Klassifikationsmodell? In welchem KNN? Welche anderen Kriterien für die Brauchbarkeit eines Modells außer dessen Vorhersagbarkeit kennst du noch?
Es gibt kein bestes Modell für alle Situationen. Die Wahl hängt von der Datenstruktur, der Anzahl der Beobachtungen und der Verteilungsannahmen ab.
- LDA: Best bei großen, gut getrennten Klassen mit gleichen Kovarianzmatrizen.
- KNN: Best bei komplexen, nichtlinearen Entscheidungsgrenzen.
Andere Kriterien:
- Interpretierbarkeit.
- Rechenaufwand.
- Robustheit gegenüber Ausreißern.
10. Warum konvergiert logistische Regression nur schlecht, wenn die Daten perfekt separiert sind?
Bei perfekter Trennung streben die Koeffizienten gegen Unendlichkeit, da das Modell versucht, die Trennung zu maximieren. Dies führt zu Problemen in der Konvergenz der Optimierung.
11. Warum ist die logistische Regression von starken Korrelationen betroffen, warum LDA und QDA nicht? Wie sieht es mit Naive Bayes und KNN aus?
Logistische Regression kann bei stark korrelierten Prädiktoren instabile Koeffizienten haben. LDA und QDA berücksichtigen die gemeinsame Verteilung und Kovarianzmatrix, was sie stabiler macht. Naive Bayes geht von unabhängigen Prädiktoren aus, daher problematisch bei Korrelationen. KNN ist weniger betroffen, da es auf Distanzen basiert.
12. Warum funktioniert die Accuracy nur schlecht als Performance-Mass, wenn eine große Imbalance in der Klassenverteilung vorliegt?
Accuracy kann irreführend sein, wenn eine Klasse stark dominiert. In diesem Fall kann ein Modell hohe Accuracy erzielen, indem es die dominierende Klasse bevorzugt, während die Leistung auf der Minderheitsklasse schlecht ist. Bessere Metriken sind Precision, Recall und der F1-Score.
LE 4: Generalisierte Lineare Modelle
1. Punkto welcher Tatsache generalisieren GLMs eigentlich? Was sind die Annahmen der linearen Regression, die möglicherweise nicht immer erfüllt sind?
GLMs generalisieren die lineare Regression, indem sie den linearen Zusammenhang zwischen den Prädiktoren und dem Erwartungswert der Antwortvariable beibehalten, aber eine breitere Palette von Verteilungen für die Antwortvariable zulassen. Annahmen der linearen Regression, die nicht immer erfüllt sind:
- Normalverteilung der Fehler
- Homoskedastizität der Fehler
- Linearität der Beziehung zwischen Prädiktoren und Antwortvariable
2. Schreibe explizit die Form eines GLM auf und beschreibe insbesondere die Rolle der Link-Funktion und den Zusammenhang zum Erwartungswert. Welche Beispiele für GLMs kennst du und welche Link-Funktionen gehören dazu?
Ein GLM hat die Form:
Die Link-Funktion ( g ) stellt eine Beziehung zwischen dem Erwartungswert ( \mathbb{E}(Y|X) ) und der linearen Kombination der Prädiktoren her.
Beispiele für GLMs und ihre Link-Funktionen:
- Logistische Regression: Logit-Link ( g(\mu) = \log\left(\frac{\mu}{1-\mu}\right) )
- Poisson-Regression: Log-Link ( g(\mu) = \log(\mu) )
- Gamma-Regression: Inverse-Link ( g(\mu) = \frac{1}{\mu} )
3. Was sind Beispiele für poissonverteilte Zielgrössen? Wie sind die Koeffizienten einer Poisson-Regression zu interpretieren? Warum hat die Link-Funktion für eine Poisson-Regression diese spezifische Form?
Beispiele für poissonverteilte Zielgrößen sind die Anzahl der Anrufe in einem Callcenter pro Stunde oder die Anzahl der Unfälle an einem bestimmten Ort pro Jahr. Die Koeffizienten einer Poisson-Regression werden als die Änderung der Log-Zählrate pro Einheit Änderung des Prädiktors interpretiert. Die Log-Link-Funktion wird verwendet, weil sie sicherstellt, dass die vorhergesagte Anzahl nicht negativ ist und die Poisson-Verteilung angemessen modelliert wird.
LE 5: Resampling
1. Erkläre den Zweck des einfachen Train-Validation-Split, eines k-fold CV-Ansatzes und LOOCV und platziere sie im Bias-Variance-Tradeoff. Welchen Wert für k würdest du im Allgemeinen für eine k-fold CV benutzen?
- Train-Validation-Split: Teilt Daten in ein Trainings- und ein Validierungsset auf. Einfach, aber kann hohe Varianz haben.
- k-fold Cross-Validation (CV): Teilt Daten in (k) gleichgroße Folds, trainiert auf (k-1) Folds und validiert auf dem verbleibenden Fold. Besseres Bias-Varianz-Verhältnis.
- Leave-One-Out Cross-Validation (LOOCV): Verwendet jede Beobachtung einmal als Validierung und den Rest als Training. Sehr niedriger Bias, aber hohe Varianz.
Empfohlener Wert für (k): 10.
2. Warum überschätzt k-fold CV den Fehler auf dem Validierungsset im Allgemeinen?
k-fold CV überschätzt den Validierungsfehler, weil das Modell auf nur (k-1) Teilen des Datensatzes trainiert wird und nicht auf dem gesamten Datensatz. Dies führt zu konservativeren Schätzungen des Fehlers.
3. Was ist der Bootstrap und wofür kann er eingesetzt werden? Kennst du ein Anwendungsbeispiel? Kannst du erklären, warum der Bootstrap funktioniert?
Der Bootstrap ist eine Methode zur Schätzung der Verteilung einer Statistik durch wiederholtes Ziehen von Stichproben mit Zurücklegen aus dem Originaldatensatz. Anwendungsbeispiel: Schätzung der Standardabweichung eines Parameters. Der Bootstrap funktioniert, weil jede Bootstrapped-Stichprobe eine repräsentative Unterstichprobe des Originaldatensatzes darstellt, wodurch die Variabilität der Statistik abgeschätzt werden kann.
4. Warum overfittest du umso stärker auf das Validierungsset, je mehr Hyperparameter-Tuning du machst?
Je mehr Hyperparameter-Tuning durchgeführt wird, desto spezifischer wird das Modell an das Validierungsset angepasst, was zu Overfitting führt. Das Modell lernt spezifische Muster und Rauschen im Validierungsset, anstatt generalisierbare Muster zu erkennen.
LE 6: Model Selection
1. Welche Methoden kennst du um eine Auswahl aus einer Menge von Prädiktoren zu treffen, die in ein Modell eingehen sollen? Welche Techniken helfen dir dabei, diese Auswahl zu treffen und so das Modell zu finden, das vermutlich am besten auf ein Testsetting generalisiert?
Methoden zur Auswahl von Prädiktoren:
- Best Subset Selection
- Forward Stepwise Selection
- Backward Stepwise Selection
- Shrinkage-Methoden (Ridge, Lasso)
- Dimension Reduction Methods (PCA, PLS)
Techniken zur Auswahl des besten Modells:
- Cross-Validation (CV)
- Information Criteria (AIC, BIC)
- Adjusted (R^2)
2. Was sind die Vor- und Nachteile von Best Subset Selection und Forward- und Backward Stepwise Selection? In welchem Setting würdest du welchen Ansatz anwenden?
- Best Subset Selection:
- Vorteile: Findet das beste Modell jeder Größe.
- Nachteile: Rechenintensiv bei großen (p).
- Setting: Kleine bis mittlere (p).
- Forward Stepwise Selection:
- Vorteile: Weniger rechenintensiv, schrittweise Prädiktoren hinzufügen.
- Nachteile: Suboptimale Modelle möglich.
- Setting: Große (p), wenn Berechnungseffizienz wichtig ist.
- Backward Stepwise Selection:
- Vorteile: Beginnt mit allen Prädiktoren, entfernt sukzessiv.
- Nachteile: Funktioniert nicht bei (n < p).
- Setting: Große (p), aber (n > p).
3. Welche Anzahl von Modellen schauen Best Subset Selection und Forward- und Backward Stepwise Selection ungefähr an, wenn eine Menge von (p) Prädiktoren vorliegt?
- Best Subset Selection: Betrachtet (2^p) Modelle.
- Forward Stepwise Selection: Betrachtet ungefähr (\frac{p(p+1)}{2}) Modelle.
- Backward Stepwise Selection: Betrachtet ungefähr (\frac{p(p+1)}{2}) Modelle.
4. Was schätzen AIC und BIC ab? Was schätzt adjusted (R^2) ab? Welche Überlegung geht in die Berechnung von adjusted (R^2) ein?
- AIC (Akaike Information Criterion): Schätzt die Qualität eines Modells hinsichtlich des Informationsverlusts:
- BIC (Bayesian Information Criterion): Schätzt die Qualität eines Modells unter Berücksichtigung der Modellkomplexität:
- Adjusted (R^2): Passt das (R^2)-Maß an die Anzahl der Prädiktoren und die Stichprobengröße an:
5. In welcher Situation kann es mehr Sinn machen, statt einem CV-Ansatz die Größen AIC, BIC oder adjusted (R^2) zu benutzen?
In Situationen mit großen Datensätzen oder bei Modellen mit vielen Prädiktoren, wo CV-Ansätze rechnerisch aufwendig sind. Auch wenn schnelle Modellvergleiche nötig sind oder bei Zeitdruck, können AIC, BIC und adjusted (R^2) nützlich sein.
6. Was ist ANOVA? Wie wird sie zur Selektion von Modellen eingesetzt?
ANOVA (Analysis of Variance) testet die Unterschiede zwischen Gruppenmittelwerten. In der Modellselektion wird ANOVA verwendet, um zu prüfen, ob das Hinzufügen zusätzlicher Prädiktoren zu einer signifikanten Verbesserung des Modells führt.
7. Was ist die One-Standard-Error-Rule? Erkläre mit einer Grafik. Warum macht sie Sinn?
Die One-Standard-Error-Rule wählt das einfachste Modell, dessen Fehler innerhalb eines Standardfehlers des minimalen Fehlerwerts liegt. Dies reduziert die Varianz und vermeidet Overfitting.
Grafik:
Fehler
^
| *
| ***
| *****
| *******
| *********
| ******************
|***********************************
--------------------------------------------> Modellkomplexität
^
Einfache Modelle innerhalb eines Standardfehlers des minimalen Fehlers
Sinn:
Die Regel sorgt für Robustheit und vermeidet Overfitting, indem sie ein einfacheres Modell bevorzugt, das fast so gut ist wie das komplexeste Modell.
LE 7: Nicht-lineare Regression
1. Welche Ansätze zur nicht-linearen Regression kennst du? Welcher ist der beste?
- Polynomial Regression
- Regression Splines
- Smoothing Splines
- Natural Splines
- Generalized Additive Models (GAMs)
- Local Regression
Es gibt keinen "besten" Ansatz; die Wahl hängt vom spezifischen Anwendungsfall und den Daten ab.
2. Ordne die verschiedenen Ansätze zur nicht-linearen Regression im Bias-Variance-Tradeoff ein - welcher ist der flexibelste?
- Höchster Bias, geringste Varianz: Polynomial Regression (niedriger Grad)
- Mittlerer Bias, mittlere Varianz: Regression Splines, Natural Splines
- Niedriger Bias, hohe Varianz: Smoothing Splines, GAMs, Local Regression (höchste Flexibilität)
3. Was sind Unterschiede zwischen einem polynomialen Regressionsmodell und einem Regression Spline?
- Polynomiale Regression: Nutzt eine einzige globale polynomiale Funktion für das gesamte Datenintervall.
- Regression Splines: Teilt das Datenintervall in mehrere Stücke und passt für jedes Stück ein Polynom an. Die Stücke sind an den Knotenpunkten verbunden und sorgen für mehr Flexibilität.
4. Worin unterscheiden sich natürliche Splines zu Regression Splines?
- Natürliche Splines: Eine spezielle Art von Regression Splines, die zusätzlich die Bedingung erfüllen, dass die zweite Ableitung an den Endpunkten null ist, was zu glatteren Kurven führt.
- Regression Splines: Allgemeinerer Ansatz ohne diese zusätzliche Bedingung.
5. Was ist eine Basisfunktion und wie wird sie in Regression Spline-Modellen angewendet?
Eine Basisfunktion ist eine grundlegende Funktion, die verwendet wird, um komplexere Funktionen zu konstruieren. In Regression Spline-Modellen werden Basisfunktionen verwendet, um die Polynomstücke in jedem Intervall darzustellen und zu kombinieren.
6. Mit welchem Parameter wird die Position eines Smoothing-Splines im Bias-Variance-Tradeoff eingestellt? Was reguliert er? Wie könntest du einen optimalen Wert für diesen Parameter bestimmen?
- Parameter: Glättungsparameter (\lambda).
- Regulierung: (\lambda) steuert das Gewicht der Glättung gegenüber der Anpassung an die Daten.
- Bestimmung: Der optimale Wert kann durch Kreuzvalidierung ermittelt werden.
7. Wie ist der Begriff ‘Freiheitsgrad’ (Degree of freedom) für Spline-Modelle zu verstehen? Was ist insbesondere der Zusammenhang der effektiven Anzahl Freiheitsgrade eines Regressionsmodells zur Spur der Projektionsmatrix, die die tatsächlichen y-Werte auf die Regressionskurve projiziert?
- Freiheitsgrad: Anzahl der unabhängigen Parameter im Modell.
- Zusammenhang: Die effektiven Freiheitsgrade eines Modells entsprechen der Spur der Projektionsmatrix, die die beobachteten Werte auf die geschätzten Werte projiziert.
8. Was ist die Truncated Power Basis und warum ist sie eine gute Basis für Regression Splines?
Die Truncated Power Basis besteht aus Basisfunktionen, die an den Knotenpunkten "abgeschnitten" werden. Sie ist eine gute Basis für Regression Splines, weil sie einfach zu konstruieren ist und gute numerische Eigenschaften aufweist.
9. Welche Ordnung der Basispolynome eines Regression-Splines würdest du standardmäßig benutzen? Bis zu welcher Ableitung muss er die Randbedingungen in den Knotenpunkten erfüllen?
Standardmäßig wird oft ein kubisches Polynom verwendet, das bis zur zweiten Ableitung stetig ist.
10. Wie funktioniert Lokale Regression? Mit welchem Parameter wird ihre Position im Bias-Variance-Tradeoff, also ihre Flexibilität eingestellt? Warum ist sie memory-basiert?
- Lokale Regression: Passt ein Modell in einem kleinen Bereich der Daten um jeden Punkt an.
- Parameter: Bandbreite oder Fenstergröße (\alpha).
- Memory-basiert: Speichert alle Datenpunkte und passt das Modell lokal an.
11. Was wird in einem GAM an der linearen Regression verallgemeinert, was nicht? Wie könntest du diese verbleibende Schwäche dennoch ein wenig mildern?
- Generalisierung: Nichtlineare Beziehungen zwischen Prädiktoren und Antwortvariable.
- Nicht generalisiert: Additive Struktur.
- Schwäche mildern: Interaktionsterme einführen.
12. Wie werden GAMs trainiert?
GAMs werden durch iteratives Glätten und Optimieren der nichtlinearen Funktionen jedes Prädiktors trainiert, häufig unter Verwendung von Backfitting.
13. Kombiniere die für GAMs und GLMs gemachten Verallgemeinerungen und schreibe die Formeln für dieses ‘GLAM’ auf.
Ein GLAM (Generalized Linear Additive Model) kombiniert die additiven nichtlinearen Funktionen von GAMs mit den flexiblen Verteilungsannahmen und Link-Funktionen von GLMs:
wobei ( g ) die Link-Funktion ist und ( f_i ) nichtlineare Funktionen der Prädiktoren sind.
Mathematische Räume im Statistischen Lernen
Was sind mathematische raueme und wie kann man sie verwenden bei machine learning?
?
Feature Raum:
- Definition: Der Feature-Raum ist der Raum, der von den Merkmalen oder Prädiktoren einer Analyse aufgespannt wird.
- Beispiel: Ein
-dimensionaler Raum , in dem jede Dimension ein Merkmal darstellt. - Verwendete Modelle: Alle Machine Learning Modelle (z.B. lineare Regression, Entscheidungsbäume)
Metrischer Raum:
- Definition: Ein Raum mit einer Distanzfunktion, die den Abstand zwischen zwei Punkten misst.
- Eigenschaften:
- Nichtnegativität:
- Identität:
wenn - Symmetrie:
- Dreiecksungleichung:
- Nichtnegativität:
- Verwendete Modelle: K-Nearest Neighbors, k-Means, hierarchisches Clustering
Vektorraum:
- Definition: Ein Raum, in dem Vektoren addiert und skaliert werden können.
- Eigenschaften:
- Abgeschlossenheit unter Addition und Skalierung
- Existenz eines Nullvektors und eines inversen Elements für jede Operation
- Assoziativität und Kommutativität der Addition
- Distributivität der Skalierung über Vektoraddition und Skalaren
- Verwendete Modelle: Lineare Regression, Hauptkomponentenanalyse (PCA)
Hilbertraum:
- Definition: Ein vollständiger innerer Produkt-Raum, wichtig für Methoden wie Kernel-Methoden und Support Vector Machines.
- Eigenschaften:
- Inneres Produkt:
definiert - Norm:
- Vollständigkeit: Jede Cauchy-Folge konvergiert
- Inneres Produkt:
- Verwendete Modelle: Support Vector Machines, Kernel PCA
Mannigfaltigkeit:
- Definition: Räume, die lokal wie ein euklidischer Raum aussehen, nützlich für nichtlineare Methoden wie t-SNE oder Isomap.
- Eigenschaften:
- Lokale Ähnlichkeit zum
- Glatte Übergangsfunktionen
- Topologische Struktur
- Lokale Ähnlichkeit zum
- Verwendete Modelle: t-SNE, Isomap, LLE (Locally Linear Embedding)
Wahrscheinlichkeitsraum:
- Definition: Ein Raum, in dem Zufallsvariablen definiert sind, grundlegend für probabilistische Modelle und maschinelles Lernen.
- Eigenschaften:
- Ereignismenge
- Wahrscheinlichkeitsmaß
- Ergebnisraum
- Ereignismenge
- Verwendete Modelle: Naive Bayes, Hidden Markov Models (HMMs), Bayesian Networks
Normalisierung und Standardisierung im Machine Learning
Wo muss man Normalisieren und Standardiseren?
?
Normalisierung:
- Definition: Skalierung der Daten auf einen Bereich von 0 bis 1.
- Verwendete Modelle:
- K-Nearest Neighbors (KNN)
- k-Means
- Neural Networks
- Begründung: Diese Modelle verwenden Distanzmetriken im metrischen Raum, und unterschiedliche Skalen der Features können die Distanzen verzerren.
Standardisierung:
- Definition: Skalierung der Daten, so dass sie einen Mittelwert von 0 und eine Standardabweichung von 1 haben.
- Verwendete Modelle:
- Lineare Regression
- Logistic Regression
- Support Vector Machines (SVM)
- Principal Component Analysis (PCA)
- Lineare Diskriminanzanalyse (LDA)
- Quadratische Diskriminanzanalyse (QDA)
- Begründung: Diese Modelle setzen voraus, dass die Features normalverteilt sind und ähnliche Skalen haben, um die Koeffizienten korrekt zu interpretieren und numerische Stabilität zu gewährleisten.
Modelle, bei denen Normalisierung oder Standardisierung nicht notwendig ist:
- Verwendete Modelle:
- Entscheidungsbäume
- Random Forests
- Gradient Boosting Trees
- Begründung: Diese Modelle sind baumbasiert und teilen die Daten an Schnittpunkten, die nicht von der Skalierung der Features beeinflusst werden.
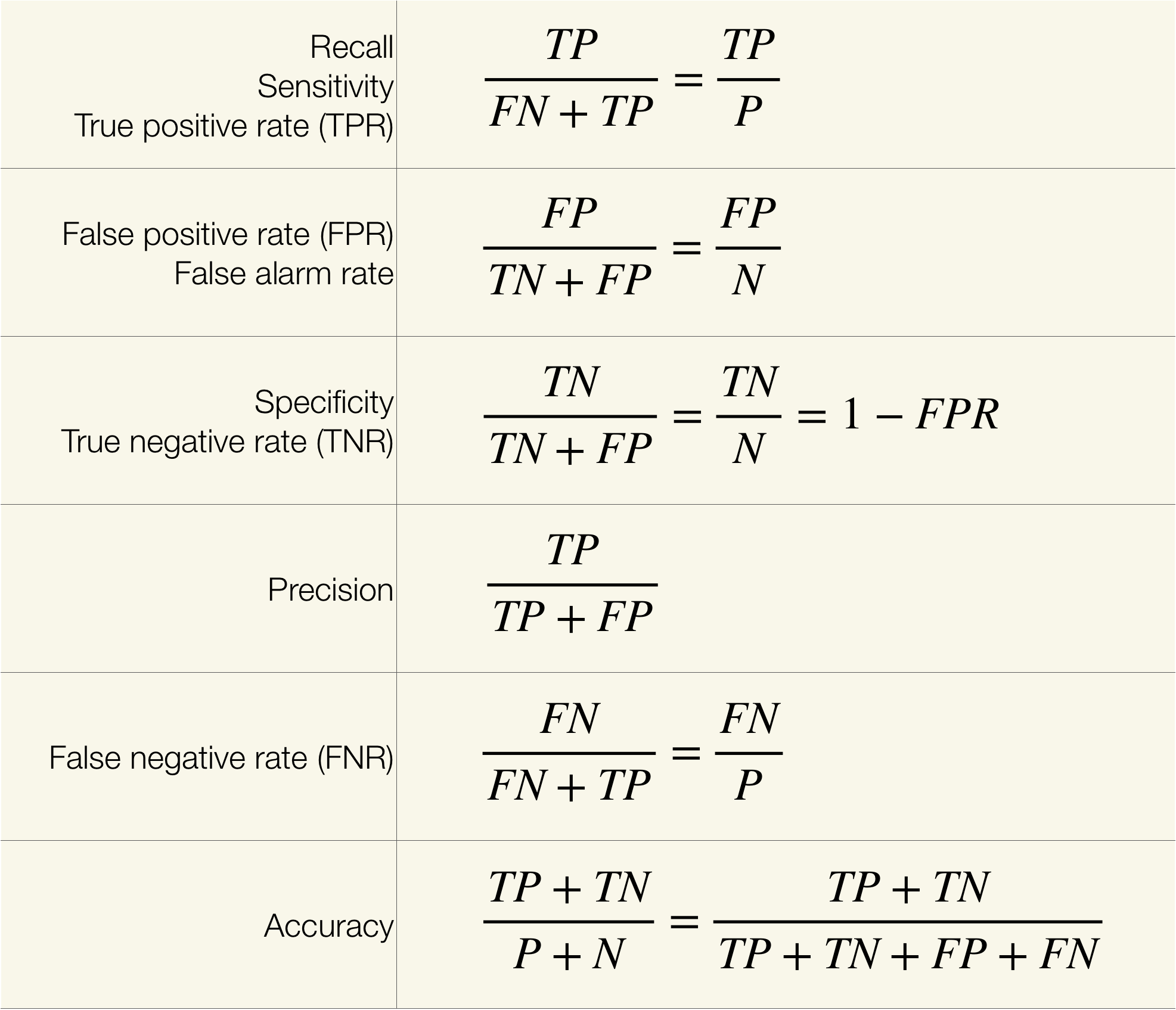
todo learn:
Wichtige Basisfunktionen in der Regressionsanalyse
1. Polynomieller Basis:
: Prädiktor : Grad des Polynoms
2. Stückweise Lineare Basisfunktionen (Piecewise Linear):
: Prädiktor : Knotenpunkt
3. Stückweise Kubische Splines:
: Prädiktor : Knotenpunkt
4. B-Splines:
: Prädiktor : Kubische B-Spline-Basisfunktion
5. Fourier-Basis:
: Prädiktor : Maximaler Frequenzindex
6. Radial Basisfunktionen (RBF):
: Prädiktor : Zentrum der RBF : Breitenparameter
7. Indicator-Basisfunktionen für Kategorische Variablen:
: Kategorischer Prädiktor : Anzahl der Kategorien
Zusammenfassung:
- Polynomiell: Einfach und gut für glatte, nichtlineare Beziehungen.
- Stückweise linear/kubisch: Flexibel, gut für Daten mit diskontinuierlichen oder nicht-glatten Strukturen.
- B-Splines: Kompakte Unterstützung, flexibel und effizient.
- Fourier-Basis: Gut für periodische Daten.
- Radial Basisfunktionen: Gut für multidimensionale, nichtlineare Beziehungen.
- Indikatorfunktionen: Für kategorische Daten.
Vergleich von Regression Splines, Smoothing Splines, GAM, GLM und Piecewise
Regression Splines:
: Beobachteter Wert : Regressionskoeffizienten : Prädiktorwert : Spline-Koeffizienten : Knotenpunkte : Fehlerterm
Smoothing Splines:
: Beobachteter Wert : Glättungsfunktion : Glätteparameter : Integervariable
Generalized Additive Models (GAM):
: Beobachteter Wert : Interzept : Glättungsfunktionen : Prädiktorwert : Fehlerterm
Generalized Linear Models (GLM):
: Antwortvariable : Linkfunktion : Regressionskoeffizienten : Prädiktorwerte
Piecewise Regression:
: Beobachteter Wert : Segment-Koeffizienten : Prädiktorwert : Segmentgrenzen
Unterschiede und Verwendung:
- Regression Splines: Flexible, segmentierte Polynomiale für nicht-glatte Strukturen.
- Smoothing Splines: Glatte Funktionen für kontinuierliche Daten; Balancierung durch
. - GAM: Additive Modelle für nichtlineare Beziehungen; interpretiert einzelne Effekte.
- GLM: Verallgemeinerung linearer Modelle; für lineare und nichtlineare, aber parametrische Beziehungen.
- Piecewise Regression: Unterschiedliche lineare Modelle in verschiedenen Bereichen; einfach und interpretierbar für verschiedene Datenbereiche.
Vergleich von Regression Splines, Smoothing Splines, GAM, GLM, Piecewise, Local Regression und Step Function Regression
Regression Splines:
: Beobachteter Wert : Regressionskoeffizienten : Prädiktorwert : Spline-Koeffizienten : Knotenpunkte : Fehlerterm
Smoothing Splines:
: Beobachteter Wert : Glättungsfunktion : Glätteparameter : Integervariable
Generalized Additive Models (GAM):
: Beobachteter Wert : Interzept : Glättungsfunktionen : Prädiktorwert : Fehlerterm
Generalized Linear Models (GLM):
: Antwortvariable : Linkfunktion : Regressionskoeffizienten : Prädiktorwerte : Fehlerterm
Piecewise Regression:
: Beobachteter Wert : Segment-Koeffizienten : Prädiktorwert : Segmentgrenzen
Local Regression (LOESS/LOWESS):
: Beobachteter Wert : Vorhergesagter Wert : Gewichtungsfunktion, die nahegelegene Beobachtungen stärker gewichtet - Annahmen: Keine spezielle funktionale Form; lokal gewichtete Regression.
- Verwendung: Flexible Anpassung an lokale Strukturen in den Daten.
Step Function Regression:
: Beobachteter Wert : Interzept : Koeffizienten für die Intervalle : Indikatorfunktion, die 1 ist, wenn im Intervall liegt, und 0 sonst : Fehlerterm - Annahmen: Daten in diskrete Intervalle unterteilt.
- Verwendung: Für Daten mit sprunghaften Änderungen.
Unterschiede und Verwendung:
- Regression Splines: Flexible, segmentierte Polynomiale für nicht-glatte Strukturen.
- Smoothing Splines: Glatte Funktionen für kontinuierliche Daten; Balancierung durch
. - GAM: Additive Modelle für nichtlineare Beziehungen; interpretiert einzelne Effekte.
- GLM: Verallgemeinerung linearer Modelle; für lineare und nichtlineare, aber parametrische Beziehungen.
- Piecewise Regression: Unterschiedliche lineare Modelle in verschiedenen Bereichen; einfach und interpretierbar für verschiedene Datenbereiche.
- Local Regression: Flexibel für lokale Strukturen; keine Annahme einer globalen Funktionalität.
- Step Function Regression: Einfach und interpretierbar für Daten mit sprunghaften Änderungen; nützlich, wenn Änderungen in bestimmten Intervallen erwartet werden.
Parametrische Modelle im Statistischen Lernen
Lineare Regression:
- Einfachstes Modell, für lineare Beziehungen.
Logistische Regression:
- Für binäre Klassifikationsprobleme.
Poisson-Regression:
- Für Zähldaten.
LDA (Lineare Diskriminanzanalyse):
- Für Klassifikationsprobleme.
QDA (Quadratische Diskriminanzanalyse):
- Für Klassifikationsprobleme mit unterschiedlichen Kovarianzmatrizen.
Ridge Regression:
- Regularisiert die lineare Regression, um Overfitting zu verhindern.
Lasso Regression:
- Setzt einige Koeffizienten auf null, was zu sparsamen Modellen führt.
Elastic Net:
- Kombination von Ridge und Lasso Regression.
Zusammenfassung:
- Lineare Modelle: Einfach und interpretierbar, für lineare Beziehungen.
- Logistische Modelle: Für Klassifikationsprobleme, log-lineare Beziehungen.
- Regularisierte Modelle (Ridge, Lasso, Elastic Net): Verhindern Overfitting, für lineare und nichtlineare Beziehungen.
- Diskriminanzanalyse (LDA, QDA): Für Klassifikationsprobleme, nutzt unterschiedliche Kovarianzmatrizen.
Weitere Parametrische Modelle im Statistischen Lernen
Bayesian Regression:
- Schätzt Parameterverteilungen statt Punktwerte.
Probit Regression:
- Für binäre Klassifikationsprobleme, ähnlich wie logistische Regression.
Multinomial Logistische Regression:
- Für mehrklassige Klassifikationsprobleme.
Negative Binomial Regression:
- Für überdisperse Zähldaten.
Ordinal Logistische Regression:
- Für geordnete kategoriale Daten.
Survival Analysis (Cox Proportional Hazards Model):
- Für Zeit-zu-Ereignis Daten.
Zusammenfassung:
- Bayesian Regression: Schätzt Verteilungen, integriert Vorwissen.
- Probit/Logit/Multinomial: Für Klassifikationsprobleme mit verschiedenen Verteilungen.
- Negative Binomial: Handhabt überdisperse Zähldaten.
- Ordinal Logistische Regression: Für geordnete Kategorien.
- Survival Analysis: Modelliert Zeit-zu-Ereignis Daten.
Annahmen der Modellsdcge im Statistischen Lernen
Regression Splines:
- Annahmen:
- Knotenauswahl: Die Positionen der Knoten müssen festgelegt werden.
- Stetige Ableitungen bis zur Ordnung
an den Knoten. - Funktionale Form innerhalb der Segmente ist polynomiell.
Smoothing Splines:
- Annahmen:
- Glätteparameter
: Balanciert Glätte und Anpassung. - Der Glättungsgrad wird durch Minimierung einer Penalisierungsfunktion bestimmt.
- Glätteparameter
Generalized Additive Models (GAM):
- Annahmen:
- Additivität: Die Gesamtfunktion ist die Summe von Glättungsfunktionen der einzelnen Prädiktoren.
- Die Glättungsfunktionen sind flexibel und können nichtlineare Beziehungen modellieren.
Generalized Linear Models (GLM):
- Annahmen:
- Lineare Form auf transformiertem Mittelwert durch eine Linkfunktion
. - Verteilung der Antwortvariable gehört zu einer Exponentialfamilie (z.B. Normalverteilung, Binomialverteilung).
- Unabhängigkeit der Beobachtungen.
- Lineare Form auf transformiertem Mittelwert durch eine Linkfunktion
Piecewise Regression:
- Annahmen:
- Diskontinuierliche Segmente: Jedes Segment hat ein eigenes lineares Modell.
- Verschiedene lineare Modelle in den Segmenten.
Bayesian Regression:
- Annahmen:
- Vorverteilungen (Priors) für die Parameter
müssen spezifiziert werden. - Posterior-Verteilung wird durch Bayes-Theorem geschätzt.
- Vorverteilungen (Priors) für die Parameter
Probit Regression:
- Annahmen:
- Die latente Variable, die die binäre Antwortvariable bestimmt, ist normalverteilt.
Multinomial Logistische Regression:
- Annahmen:
- Für mehrklassige Klassifikationsprobleme.
- Unabhängigkeit der irrelevanten Alternativen (IIA).
Negative Binomial Regression:
- Annahmen:
- Verwendet für überdisperse Zähldaten.
- Varianz ist größer als der Mittelwert (Overdispersion).
Ordinal Logistische Regression:
- Annahmen:
- Für geordnete kategoriale Daten.
- Proportional Odds Annahme: Die Verhältniswahrscheinlichkeiten sind für alle Kategorien gleich.
Survival Analysis (Cox Proportional Hazards Model):
- Annahmen:
- Proportional Hazards Annahme: Die Hazard-Raten der Gruppen sind proportional.
- Keine Zeitabhängigkeit der Hazard-Raten.
Zusammenfassung:
- Regression Splines: Knotenauswahl, stetige Ableitungen.
- Smoothing Splines: Glätteparameter, Minimierung einer Penalisierungsfunktion.
- GAM: Additivität, flexible Glättungsfunktionen.
- GLM: Lineare Form durch Linkfunktion, Verteilung aus Exponentialfamilie, Unabhängigkeit der Beobachtungen.
- Piecewise Regression: Diskontinuierliche Segmente, verschiedene lineare Modelle.
- Bayesian Regression: Spezifikation von Priors, Bayes-Theorem zur Schätzung.
- Probit Regression: Normalverteilung der latenten Variable.
- Multinomial Logistische Regression: Unabhängigkeit der irrelevanten Alternativen.
- Negative Binomial Regression: Überdispersion der Zähldaten.
- Ordinal Logistische Regression: Proportional Odds Annahme.
- Survival Analysis: Proportional Hazards Annahme, keine Zeitabhängigkeit.
Heteroskedastizität in der Linearen Regression
Definition:
Heteroskedastizität liegt vor, wenn die Varianz der Fehlerterme ((\epsilon_i)) in einem Regressionsmodell nicht konstant ist, sondern von den Werten der unabhängigen Variablen abhängt.
Modellannahmen der linearen Regression:
Ein zentrales Modellannahme in der linearen Regression ist die Homoskedastizität, das bedeutet, dass die Varianz der Fehlerterme konstant ist:
Folgen von Heteroskedastizität:
Verzerrte Standardfehler: Die Schätzer für die Standardfehler der Regressionskoeffizienten sind verzerrt, was zu inkorrekten Konfidenzintervallen und Hypothesentests führen kann.
Ineffiziente Schätzer: Die Regressionskoeffizienten bleiben unverzerrt, aber sie sind nicht die effizientesten Schätzer.
Methoden zur Korrektur von Heteroskedastizität:Transformation der abhängigen Variable:
- Log-Transformation: Kann die Varianz stabilisieren.
- Quadratische oder andere nichtlineare Transformationen.
Verwendung robuster Standardfehler:
- Anpassung der Standardfehler der Koeffizientenschätzer, um die Verzerrung durch Heteroskedastizität zu kompensieren.
Generalized Least Squares (GLS):
- Transformation des Modells, um die Varianz der Fehlerterme zu stabilisieren.
Weighted Least Squares (WLS):
- Gewichtung der Beobachtungen mit der inversen Varianz der Fehlerterme, um die Effizienz der Schätzer zu verbessern.
Literatur und weitere Informationen:
- "An Introduction to Statistical Learning" beschreibt diese Methoden detailliert und zeigt Beispiele, wie man sie anwendet【253†source】.
- Weitere Erklärungen und technische Details finden sich in "Applied Regression Analysis" von Draper und Smith.
Cheat sheet to learn:
Modelle im Statistischen Lernen
1. Linear Regression
-
Simple Linear Regression:
- Formel:
- Eigenschaften: Modelliert die lineare Beziehung zwischen zwei Variablen.
- Annahmen: Lineare Beziehung, Unabhängigkeit der Fehler, Normalverteilung der Fehler, Homoskedastizität.
- Degree of Freedom (DF):
- Verteilung: Normalverteilung der Fehler
- Größen:
: Antwortvariable : Interzept : Steigung : Prädiktor : Fehlerterm
- Formel:
-
Multiple Linear Regression:
- Formel:
- Eigenschaften: Erweiterung der einfachen linearen Regression auf mehrere Prädiktoren.
- Annahmen: Gleiche wie bei einfacher linearer Regression.
- Degree of Freedom (DF):
- Verteilung: Normalverteilung der Fehler
- Größen:
: Antwortvariable : Regressionskoeffizienten : Prädiktoren : Fehlerterm
- Formel:
2. Classification
-
Logistic Regression:
- Formel:
- Eigenschaften: Modelliert die Wahrscheinlichkeit eines binären Outcomes.
- Annahmen: Logit-Funktion ist linear in den Prädiktoren.
- Degree of Freedom (DF):
- Verteilung: Binomialverteilung der Antwortvariable
- Größen:
: Wahrscheinlichkeit des Ereignisses : Regressionskoeffizienten : Prädiktoren
- Formel:
-
Linear Discriminant Analysis (LDA):
- Formel:
- Eigenschaften: Findet lineare Kombinationen der Prädiktoren, die die Klassen am besten trennen.
- Annahmen: Multivariate Normalverteilung der Prädiktoren, gleiche Kovarianzmatrix für alle Klassen.
- Degree of Freedom (DF):
- Verteilung: Multivariate Normalverteilung
- Größen:
: Diskriminanzfunktion für Klasse : Prädiktorvektor : Kovarianzmatrix : Mittelwertvektor der Klasse : A-priori Wahrscheinlichkeit der Klasse
- Formel:
-
Quadratic Discriminant Analysis (QDA):
- Formel:
- Eigenschaften: Erweiterung von LDA, erlaubt unterschiedliche Kovarianzmatrizen für jede Klasse.
- Annahmen: Multivariate Normalverteilung der Prädiktoren.
- Degree of Freedom (DF):
- Verteilung: Multivariate Normalverteilung
- Größen:
: Diskriminanzfunktion für Klasse : Prädiktorvektor : Kovarianzmatrix der Klasse : Mittelwertvektor der Klasse : A-priori Wahrscheinlichkeit der Klasse
- Formel:
-
K-Nearest Neighbors (KNN):
- Eigenschaften: Klassifiziert neue Datenpunkte basierend auf den
nächsten Nachbarn im Trainingsdatensatz. - Annahmen: Keine spezifischen Verteilungsannahmen, nicht-parametrisch.
- Degree of Freedom (DF): Effektive Freiheitsgrade variieren je nach
- Verteilung: Nicht parametrisch
- Größen:
: Anzahl der nächsten Nachbarn
- Eigenschaften: Klassifiziert neue Datenpunkte basierend auf den
-
Naive Bayes:
- Formel:
- Eigenschaften: Annahme der Unabhängigkeit der Prädiktoren gegeben die Klassen.
- Annahmen: Bedingte Unabhängigkeit der Prädiktoren.
- Degree of Freedom (DF): Variiert je nach Anzahl der Klassen und Prädiktoren.
- Verteilung: Unterschiedlich je nach Art des Naive Bayes Modells (z.B. Gaussian, Multinomial)
- Größen:
: Posteriori Wahrscheinlichkeit der Klasse : Likelihood der Prädiktoren gegeben die Klasse : A-priori Wahrscheinlichkeit der Klasse
- Formel:
3. Linear Model Selection and Regularization
Subset Selection:
- Eigenschaften: Wählt eine Untermenge der Prädiktoren aus, die das Modell optimiert.
- Annahmen: Gleich wie bei der linearen Regression.
- Degree of Freedom (DF): Anzahl der ausgewählten Prädiktoren.
- Verteilung: Normalverteilung der Fehler.
- Größen:
: Anzahl der ausgewählten Prädiktoren Shrinkage Methods (Ridge Regression, Lasso):
Ridge Regression:
- Formel:
- Eigenschaften: Fügt einen L2-Penalisierungsterm hinzu, um die Koeffizienten zu schrumpfen.
- Annahmen: Gleich wie bei der linearen Regression.
- Degree of Freedom (DF):
- Verteilung: Normalverteilung der Fehler.
- Größen:
: Regularisierungsparameter Lasso:
- Formel:
- Eigenschaften: Fügt einen L1-Penalisierungsterm hinzu, kann Koeffizienten auf null setzen.
- Annahmen: Gleich wie bei der linearen Regression.
- Degree of Freedom (DF):
- Verteilung: Normalverteilung der Fehler.
- Größen:
: Regularisierungsparameter 5. Non-linear Models
Polynomial Regression:
- Formel:
- Eigenschaften: Modelliert nicht-lineare Beziehungen durch Hinzufügen von Potenztermen des Prädiktors.
- Annahmen: Gleiche wie bei der linearen Regression.
- Degree of Freedom (DF):
- Verteilung: Normalverteilung der Fehler
- Größen:
: Antwortvariable : Regressionskoeffizienten : Prädiktor : Fehlerterm : Grad des Polynoms Step Functions:
- Formel:
- Eigenschaften: Teilt den Prädiktorraum in Intervalle und passt eine konstante Funktion in jedem Intervall an.
- Annahmen: Gleiche wie bei der linearen Regression.
- Degree of Freedom (DF):
- Verteilung: Normalverteilung der Fehler
- Größen:
: Antwortvariable : Regressionskoeffizienten : Prädiktor : Indikatorfunktion : Schwellenwerte Regression Splines:
- Formel:
- Eigenschaften: Fügt Knotensplines hinzu, um Flexibilität zu erhöhen.
- Annahmen: Gleiche wie bei der linearen Regression.
- Degree of Freedom (DF):
- Verteilung: Normalverteilung der Fehler
- Größen:
: Antwortvariable : Regressionskoeffizienten : Prädiktor : Koeffizienten der Knotensplines : Knotenpunkte Natural Splines:
- Formel:
- Eigenschaften: Eine spezielle Art von Regression Splines, die natürliche Randbedingungen haben, um die Flexibilität am Rand des Datenbereichs zu reduzieren.
- Annahmen: Gleiche wie bei der linearen Regression.
- Degree of Freedom (DF): Abhängig von der Anzahl der Knoten und der Ordnung der Splines
- Verteilung: Normalverteilung der Fehler
- Größen:
: Antwortvariable : Regressionskoeffizienten : Basisfunktionen der natürlichen Splines : Fehlerterm Smoothing Splines:
- Formel:
- Eigenschaften: Nutzt einen Glätteparameter
, um die Glätte der Anpassung zu regulieren. - Annahmen: Gleich wie bei der linearen Regression.
- Degree of Freedom (DF):
- Verteilung: Normalverteilung der Fehler
- Größen:
: Antwortvariable : Regressionskoeffizienten : Smoothing Splines Basisfunktionen : Glätteparameter : Fehlerterm Local Regression:
- Formel:
- Eigenschaften: Passt einfache Modelle (z.B. lineare Regression) in einem gleitenden Fenster der Daten an.
- Annahmen: Keine spezifischen Verteilungsannahmen, nicht-parametrisch.
- Degree of Freedom (DF):
- Verteilung: Nicht-parametrisch
- Größen:
: Antwortvariable : Gewichte der lokalen Regression : Beobachtungen Generalized Additive Models (GAMs):
- Formel:
- Eigenschaften: Additive Modelle, die nicht-lineare Funktionen der Prädiktoren verwenden.
- Annahmen: Additivität der Effekte der Prädiktoren.
- Degree of Freedom (DF): Summe der Freiheitsgrade der einzelnen
- Verteilung: Normalverteilung der Fehler
- Größen:
: Antwortvariable : Interzept : Glättungsfunktionen : Fehlerterm
6. Unsupervised Learning
Principal Component Analysis (PCA):
- Formel:
- Eigenschaften: Reduziert die Dimension der Daten, indem sie orthogonale Hauptkomponenten extrahiert.
- Annahmen: Keine spezifischen Verteilungsannahmen.
- Degree of Freedom (DF): Anzahl der Hauptkomponenten
- Verteilung: Nicht-parametrisch
- Größen:
: Hauptkomponenten : Ursprüngliche Daten : Gewichte der Hauptkomponenten K-Means Clustering:
- Formel: Minimiert die Summe der quadrierten Distanzen zwischen Datenpunkten und dem nächstgelegenen Clusterzentrum
- Eigenschaften: Partitioniert die Daten in
Cluster. - Annahmen: Keine spezifischen Verteilungsannahmen.
- Degree of Freedom (DF): Anzahl der Cluster
- Verteilung: Nicht-parametrisch
- Größen:
: Anzahl der Cluster Hierarchical Clustering:
- Formel: Dendrogramm-basierte Darstellung der Datencluster
- Eigenschaften: Bildet eine hierarchische Struktur der Datencluster.
- Annahmen: Keine spezifischen Verteilungsannahmen.
- Degree of Freedom (DF): Abhängig von der Höhe der Hierarchie
- Verteilung: Nicht-parametrisch
- Größen:
: Höhe des Dendrogramms
todo:
- generative vs discriminative beispiel mit smote
- bayes lda qda

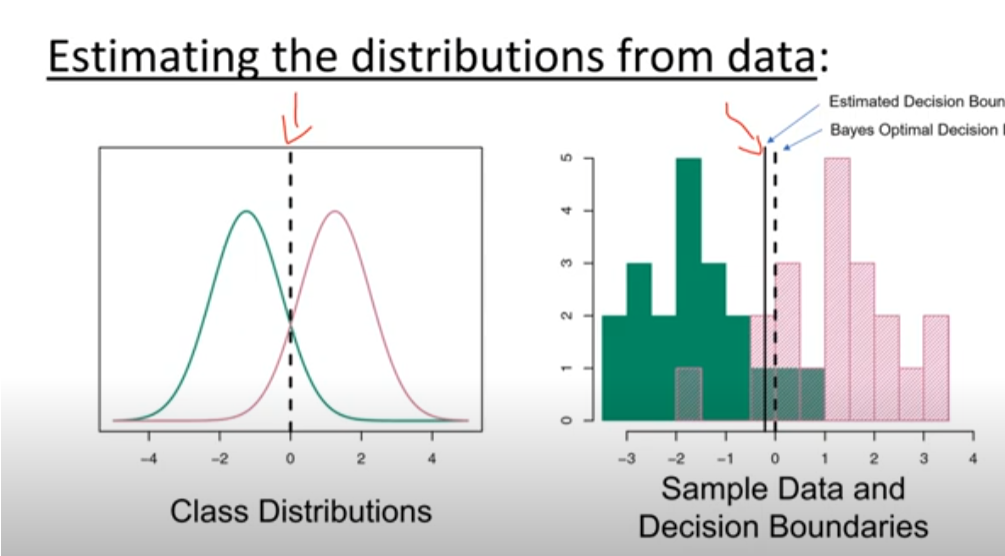
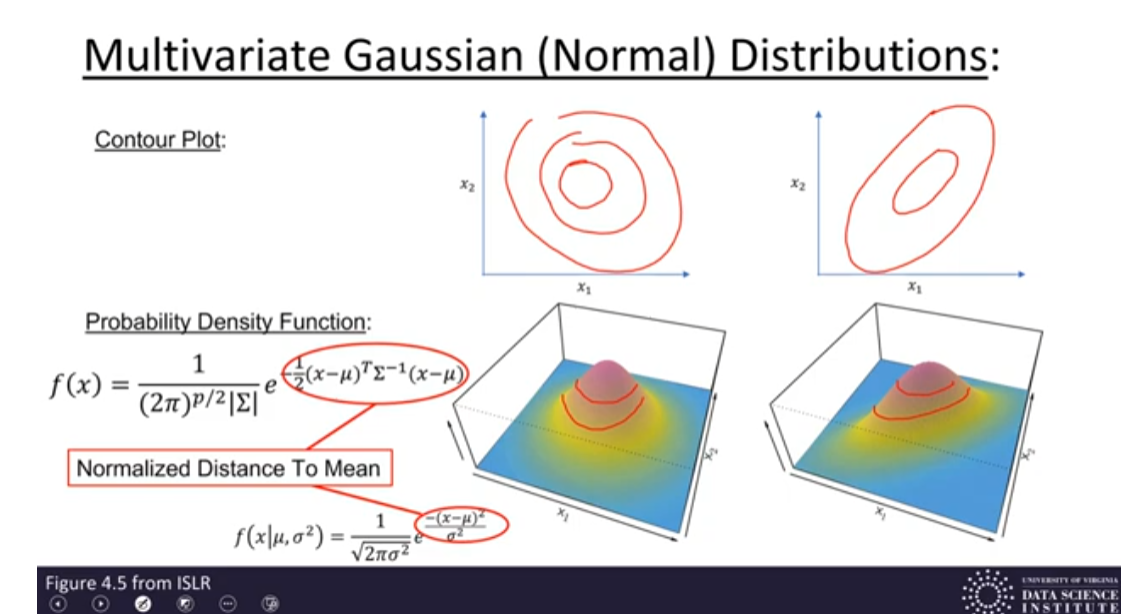

quick learning:
Naive Bayes Klassifikator: Formel und Annahmen
Formel
Der Naive Bayes Klassifikator nutzt das Bayes-Theorem:
[ P(C|X) \propto P(C) \prod_{i=1}^{n} P(x_i|C) ]
Dabei steht ( C ) für die Klasse und ( X = (x_1, x_2, \ldots, x_n) ) für die Merkmale. Die Vorhersage erfolgt durch Maximierung:
[ \hat{C} = \arg\max_C P(C) \prod_{i=1}^{n} P(x_i|C) ]
Annahmen
-
Bedingte Unabhängigkeit:
- Jedes Merkmal ( x_i ) ist unabhängig von den anderen Merkmalen ( x_j ) gegeben die Klasse ( C ).
-
Gleiche Wichtigkeit aller Merkmale:
- Alle Merkmale tragen unabhängig voneinander zur Klassifizierung bei.
Diese Annahmen vereinfachen die Berechnungen erheblich und ermöglichen effiziente Klassifizierungsalgorithmen.
Gesetzt der Kontinuitaet
ähnliche Dinge sind näher bei einander und unähnliche Dinge sind weiter ausseinander
ETC
-
Naive Bayes hat als annahme, dass alle Klassen unabhähgig von einande sind.
-
LDA hat als annhame, dass die Merkmale/Beobachtungen normalverteilt in den einzelnen Klassen sind. Ausserdem nimmt LDA an, dass alle Klassen die gleiche Kovarianz Matrix haben. Descion boundires sind linear.
-
QDA ist wie LDA auch annahme merkamle in den einzelnen Klassen normalverteilt und jetzt noch die annahme, dass jede Klasse ihre eigene Kovarianz Matrix haben kann. Dadurch koennen die Descion Boundries quadratisch sein.
-
Dikriminative Modelle trainieren die desicion boundry um die Klassen zu trennen.
-
Generative Modelle trainieren die Warscheinlichverteilungsfunktion, um die Descion Boundries aufzustellen.
-
Die Maximum Likelihood bei der Linearen Regression besagt, dass man zu den fitt waehlen soll also so die fehler minimieren, dass man alle Punkte in der normalverteilung bei der hoechsten wahrscheinlichkeit hat.
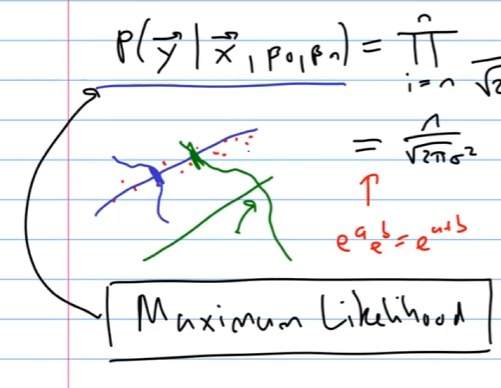

-
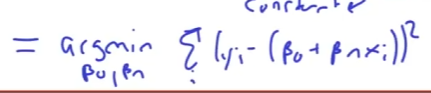
LR annahmen: Residuen normalverteilt, erwartungswert 0, linearitaet des fs, unabhaegigkeit der einzelnen Samples, keine Kolinearitat, konstante variance
-
Der P Wert gibt an wie unwahrschienlich es ist, dass etwas zufaellig passiert ist wenn p 0.05 kann die H0 hyptothese verworfen werden.
-
F-Statistic um zu ueber pruefen ob irgendeine parameter signifikant ist also besser als kein modell.
-
Prediction interval berechnet, die unsicherheit des modelles und die unsicherheit der daten
-
Die Additivitaet kann man auflockern mit interaktionen von dummy variablen
-
hierachische prinzip, man muss die haupteffecte drinnen lassen auf wenn nicht significatin von bei den interactionen.
-
Heteroskedazitaet die Fehler sind abhaegig von dem y
-
homoskedazitaet die Fehler sind unabhaegig von dem Y wert
-
high leverage points sind aussreisser, die nicht mehr in der verteilung der praedictoren sind.
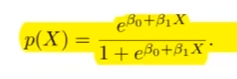
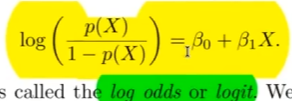
log odds macht einen werte bereich zwischen minus unedlich und unedlich.
- Die Parameter in der Logistischen Funktion ändern nun nicht die Y anhängige variable sondern die odds . Das heisst negative beta kleinere odds heisst kleinere wahrscheinlichkeiten.
- Confounding: Zusammenhang von Korrelation und Kausalitaet, wir modelieren nie kausalitaet
Softmax bringt alle auf 1
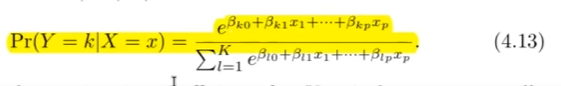
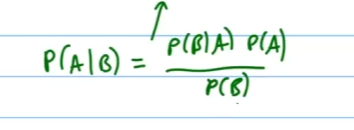

dieses f_k(x) muss jetzt modlliert werden.
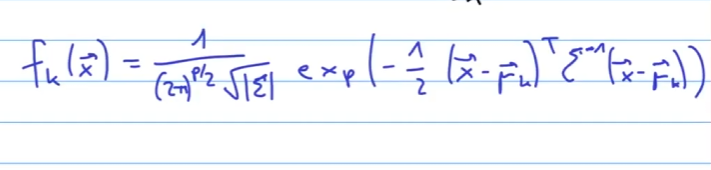

QDA und LDA kann man dann in das bayesche theorem einsetzen:
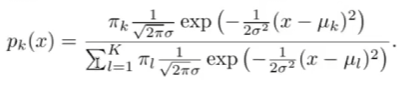
Naive bayes --> naive weil nimmt eine annahme dass alle klassen unabhaegig sind.
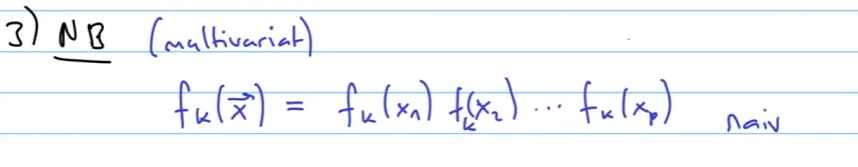
Naive bayes ist wie LDA aber mit einer diagonal matrix sigma
poisson verteilung: